题目内容
设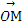 =(1,1),
=(1,1),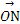 =(3,1),O为坐标原点,动点P(x,y)满足0≤
=(3,1),O为坐标原点,动点P(x,y)满足0≤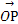 ·
·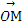 ≤1,0≤
≤1,0≤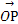 ·
·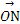 ≤1,则
≤1,则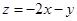 的最大值是 ( )
的最大值是 ( )
| A.0 | B.1 | C. | D. |
A
解析试题分析: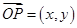 ,
,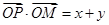 ,
,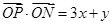 ,即
,即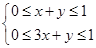 ,画出可行域如图
,画出可行域如图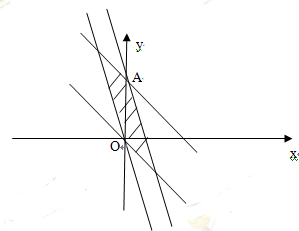
平移目标函数线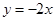 ,使之经过可行域当过
,使之经过可行域当过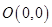 时纵截距最小此时
时纵截距最小此时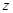 最大为0。故A正确。
最大为0。故A正确。
考点:1向量数量积;2线性规划问题。

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
平面向量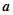 与
与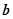 的夹角为60°,
的夹角为60°,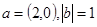 ,则
,则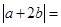 ( )
( )
A.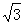 | B. | C.4 | D.12 |
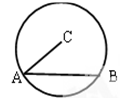
如图,半径为R的圆C中,已知弦AB的长为5,则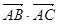 =( )
=( )
A.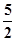 | B.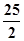 | C.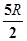 | D.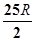 |
设向量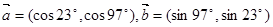 ,则
,则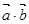 等于 ( )
等于 ( )
A.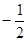 | B.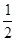 | C. | D.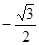 |
已知向量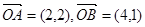 ,点P在
,点P在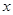 轴上,
轴上,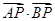 取最小值时P点坐标是( )
取最小值时P点坐标是( )
A.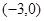 | B.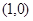 | C.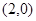 | D.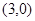 |
在 中,
中, ( )
( )
A. | B. | C. | D. |
[2013·重庆诊测]若向量a=(1,λ,2),b=(2,-1,2),且a与b的夹角余弦值为 ,则λ等于( )
,则λ等于( )
| A.2 | B.-2 | C.-2或 | D.2或- |
对任意两个非零的平面向量α和β,定义 .若两个非零的平面向量
.若两个非零的平面向量 和
和 ,满足
,满足 与
与 的夹角
的夹角 ,且
,且 和
和 都在集合
都在集合 中,则
中,则 =
=
A. | B. | C.1 | D. |
 ,则
,则 的夹角为( )
的夹角为( )


