题目内容
从装有大小相同的3个白球和3个红球的袋中做摸球试验,每次摸出一个球.如果摸出白球,则另从袋外取一个红球替换该白球放回袋中,继续做下一次摸球试验;如果摸出红球,则结束摸球试验.
(Ⅰ)求一次摸球后结束试验的概率P1与两次摸球后结束试验的概率P2;
(Ⅱ)记结束试验时的摸球次数为ξ,求ξ的分布列及其数学期望Eξ.
解:(Ⅰ)一次摸球结束试验,即摸出红球,故概率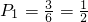 ;
;
二次摸球结束试验,先摸出白球,再摸出红球故概率P2= ;
;
(Ⅱ)依题意得:ξ的所有可能值有1,2,3,4
 ,
,
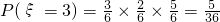 ;
;  ;
;
∴Eξ=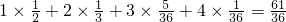 .
.
分析:(Ⅰ)一次摸球后结束试验,即摸出红球;两次摸球后结束试验,即先摸出白球,再摸出红球,故可求概率;
(Ⅱ)确定结束试验时的摸球次数为ξ的可能取值,求出概率,即可求ξ的分布列及其数学期望Eξ.
点评:本题考查古典概型互斥事件和独立事件的概率,随机变量的分布列及数学期望等知识与方法;考查运算求解能力以及应用概率知识分析解决问题的能力;考查必然与或然思想.
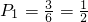 ;
;二次摸球结束试验,先摸出白球,再摸出红球故概率P2=
 ;
; (Ⅱ)依题意得:ξ的所有可能值有1,2,3,4
 ,
,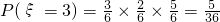 ;
;  ;
; | ξ | 1 | 2 | 3 | 4 |
| P |  |  |  |  |
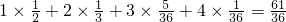 .
.分析:(Ⅰ)一次摸球后结束试验,即摸出红球;两次摸球后结束试验,即先摸出白球,再摸出红球,故可求概率;
(Ⅱ)确定结束试验时的摸球次数为ξ的可能取值,求出概率,即可求ξ的分布列及其数学期望Eξ.
点评:本题考查古典概型互斥事件和独立事件的概率,随机变量的分布列及数学期望等知识与方法;考查运算求解能力以及应用概率知识分析解决问题的能力;考查必然与或然思想.

练习册系列答案
相关题目