题目内容
 本题满分13分
本题满分13分 如图,三角形ABC中,AC=BC=
如图,三角形ABC中,AC=BC= ,ABED是边长为1
,ABED是边长为1
的正方形,平面ABED⊥底面ABC,若G、F分别是EC、BD的中点.
(I)求证:GF//底面ABC;
(Ⅱ)求证:AC⊥平面EBC;
(Ⅲ)求几何体ADEBC的体积V.

【答案】
又∵ADEB为正方形
∴DE//AB,从而HF//AB
解:(I)证法一:取BE的中点H,连结HF、GH,(如图1)
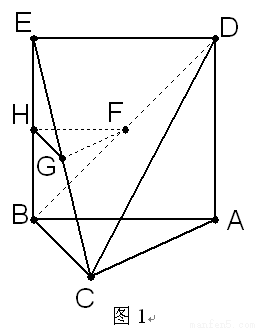
∵G、F分别是EC和BD的中点
∴HG//BC,HF//DE,……………… 2分
|
∴HF//平面ABC,HG//平面ABC, HF∩HG=H,
∴平面HGF//平面ABC
∴GF//平面ABC………………4分
(Ⅱ)∵ADEB为正方形,∴EB⊥AB,∴GF//平面AB………………5分
又∵平面ABED⊥平面ABC,∴BE⊥平面ABC ………………6分
∴BE⊥AC
又∵CA2+CB2=AB2
∴AC⊥BC,
∵BC∩BE=B,
∴AC⊥平面BCE ………………8分
(Ⅲ)连结CN,因为AC=BC,∴CN⊥AB, ……………… 9分
又平面ABED⊥平面ABC,CN平面ABC,∴CN⊥平面ABED。……………… 10分
∵三角形ABC是等腰直角三角形,∴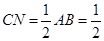 ,
………………11分
,
………………11分
∵C—ABED是四棱锥,
∴VC—ABED=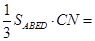
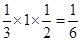 ………………13分
………………13分
【解析】略

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
 (本题满分13分) 如图所示,质点P在正方形ABCD的四个顶点上按逆时针方向前进.现在投掷一个质地均匀、每个面上标有一个数字的正方体玩具,它的六个面上分别写有两个1、两个2、两个3一共六个数字.质点P从A点出发,规则如下:当正方体上底面出现的数字是1,质点P前进一步(如由A到B);当正方体上底面出现的数字是2,质点P前进两步(如由A到C),
(本题满分13分) 如图所示,质点P在正方形ABCD的四个顶点上按逆时针方向前进.现在投掷一个质地均匀、每个面上标有一个数字的正方体玩具,它的六个面上分别写有两个1、两个2、两个3一共六个数字.质点P从A点出发,规则如下:当正方体上底面出现的数字是1,质点P前进一步(如由A到B);当正方体上底面出现的数字是2,质点P前进两步(如由A到C),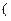 本题满分13分
本题满分13分 如图,三角形ABC中,AC=BC=
如图,三角形ABC中,AC=BC= ,ABED是边长为1
,ABED是边长为1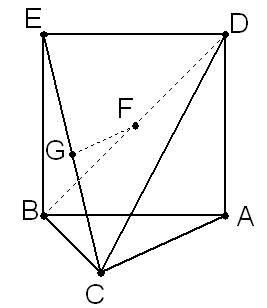
 中,
中, 平面
平面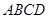 ,
,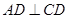 ,
,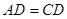 ,
,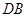 平分
平分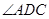 ,
,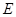 为
为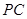 的中点.
的中点.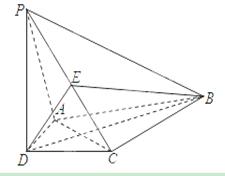
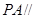 平面
平面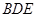 ;
;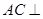 平面
平面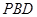 .
. 中,平面
中,平面 ∥平面
∥平面 ,
, ,
, ,
,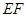 ∥
∥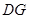 .且
.且 ,
, .
. ∥平面
∥平面 ;
; 的余弦值;
的余弦值;