题目内容
如果z=a+bi(a,b∈R,且a≠0)是虚数,则z,. |
| z |
. |
| z |
. |
| z |
分析:根据所给的复数的表示式,分别写出八个不同的表示形式,对于这八个形式进行比较,得到虚数、实数和相等的对数.
解答:解:∵z=a+bi(a,b∈R,且a≠0),
∴
=a-bi,
=a+bi,|z|=
,
|
|=
,z-
=2bi,
z2=(a2-b2)+2abi,
|z|2=a2+b2,|z2|=a2+b2,
∴有4个虚数,有4个实数,相等的有3组.
故答案为:4;4;3
∴
. |
| Z |
. | ||
|
| a2+b2 |
|
. |
| z |
| a2+b2 |
. |
| z |
z2=(a2-b2)+2abi,
|z|2=a2+b2,|z2|=a2+b2,
∴有4个虚数,有4个实数,相等的有3组.
故答案为:4;4;3
点评:本题主要考查复数的运算,包括求共轭复数,模长,平方,减法运算,实际上复数的加减乘除运算是比较简单的问题,在高考时有时会出现,若出现则是要我们一定要得分的题目.

练习册系列答案
相关题目
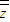 ,|z|,|
,|z|,|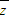 |,z-
|,z-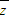 ,z2,|z|2,|z2|中是虚数的有 个,是实数的有 个,相等的有 组.
,z2,|z|2,|z2|中是虚数的有 个,是实数的有 个,相等的有 组.