题目内容
在△ABC中,m=(cos(1)求C;
(2)已知c=![]() ,△ABC的面积为S=
,△ABC的面积为S=![]() ,求a+b.
,求a+b.
思路解析:此题主要考查向量的数量积与解三角形的知识,使解三角形不再孤立,也体现了向量的工具性作用.(1)已知两向量的夹角,运用数量积来求C.(2)已知面积,利用面积公式求出a与b的积,再利用余弦定理来求a2+b2,进而求出a+b.
解:(1)∵m=(cos![]() ,sin
,sin![]() ),n=(cos
),n=(cos![]() ,-sin
,-sin![]() ),
),
∴m·n=cos2![]() -sin2
-sin2![]() =cosC.
=cosC.
又m·n=|m|·|n|cos![]() =1×1×
=1×1×![]() =
=![]() ,
,
∴cosC=![]() .∴C=
.∴C=![]() .
.
(2)∵c2=a2+b2-2abcosC,c=![]() ,
,
∴![]() =a2+b2-ab=(a+b)2-3ab.
=a2+b2-ab=(a+b)2-3ab.
∵S△ABC=![]() absinC=
absinC=![]() absin
absin![]() =
=![]() ab=
ab=![]() ,
,
∴ab=6.
从而(a+b)2=![]() +3ab=
+3ab=![]() +18=
+18=![]() ,∴a+b=
,∴a+b=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ABC中,M是BC的中点,AM ="3,BC" =10,则
ABC中,M是BC的中点,AM ="3,BC" =10,则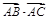 =______________
=______________