题目内容
某人上午7：00乘汽车以v1千米/小时（30≤v1≤100）匀速从A地出发到距300公里的B地，在B地不作停留，然后骑摩托车以v2千米/小时（4≤v2≤20）匀速从B地出发到距50公里的C地，计划在当天16：00至21：00到达C地．设乘汽车、骑摩托车的时间分别是x，y小时，如果已知所需的经费p=100+3（5-x）+2（8-y）元，那么v1，v2分别是多少时走的最经济，此时花费多少元？
【答案】分析：先建立满足题意的约束条件及目标函数，作出满足条件的x，y的区域，利用几何意义可求目标函数的最小值
解答：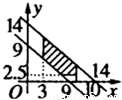
解：由题意得，
，
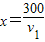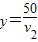
∵30≤v1≤100，4≤v2≤20
∴
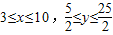
由题设中的限制条件得9≤x+y≤14
于是得约束条件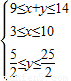
目标函数p=100+3（5-x）+2（8-y）=131-3x-2y（6分）
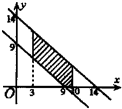
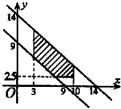
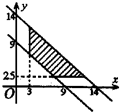
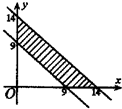
做出可行域（如图），
当
平行移动到过（10，4）点时纵截距最大，此时p最小．
所以当x=10，y=4，即v1=30，v2=12.5时，pmin=93元 （12分）
（没有图扣2分）
点评：本题考查简单线性规划的应用，解题的关键是理解简单线性规划的意义及其原理，解题步骤，本题的难点是建立线性约束条件及确定线性目标函数，本题考查了数形结合的思想及转化的思想．
解答：
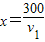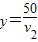
解：由题意得，，∵30≤v1≤100，4≤v2≤20
∴
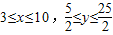
由题设中的限制条件得9≤x+y≤14
于是得约束条件
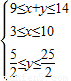
目标函数p=100+3（5-x）+2（8-y）=131-3x-2y（6分）
做出可行域（如图），
当
平行移动到过（10，4）点时纵截距最大，此时p最小．所以当x=10，y=4，即v1=30，v2=12.5时，pmin=93元 （12分）
（没有图扣2分）
点评：本题考查简单线性规划的应用，解题的关键是理解简单线性规划的意义及其原理，解题步骤，本题的难点是建立线性约束条件及确定线性目标函数，本题考查了数形结合的思想及转化的思想．
练习册系列答案
优学名师名题系列答案
相关题目
