题目内容
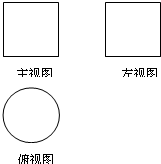
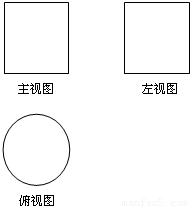
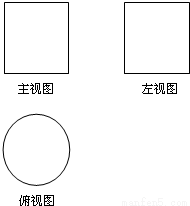
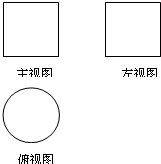 (文)如图所示,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的全面积为
(文)如图所示,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的全面积为| 3 |
| 2 |
| 3 |
| 2 |
(理)某学校要从5名男生和2名女生中选出2人作为上海世博会志愿者,若用随机变量ξ表示选出的志愿者中女生的人数,则数学期望Eξ=
| 4 |
| 7 |
| 4 |
| 7 |
(结果用最简分数表示)
分析:(文)由题意可得:几何体是一个圆柱,并且圆柱的底面是一个直径为1的圆,圆柱的高是1,再根据有关的公式计算出答案即可.
(理)由题意可得:ξ可能取的值为0,1,2,再分别求出其发生的概率,进而根据有关的公式求出期望.
(理)由题意可得:ξ可能取的值为0,1,2,再分别求出其发生的概率,进而根据有关的公式求出期望.
解答:解:(文)由三视图可得几何体是一个圆柱,并且得到圆柱的底面是一个直径为1的圆,圆柱的高是1,
所以圆柱的全面积是2×π (
)2+2 π×
×1=
.
(理)由题意可得:ξ可能取的值为0,1,2,
∴P(ξ=0)=
=
,
P(ξ=1)=
=
,
P(ξ=2)=
=
,
∴Eξ=0×
+1×
+2×
=
.
故答案为:
;
.
所以圆柱的全面积是2×π (
| 1 |
| 2 |
| 1 |
| 2 |
| 3π |
| 2 |
(理)由题意可得:ξ可能取的值为0,1,2,
∴P(ξ=0)=
| ||
|
| 10 |
| 21 |
P(ξ=1)=
| ||||
|
| 10 |
| 21 |
P(ξ=2)=
| ||
|
| 1 |
| 21 |
∴Eξ=0×
| 10 |
| 21 |
| 10 |
| 21 |
| 1 |
| 21 |
| 4 |
| 7 |
故答案为:
| 3π |
| 2 |
| 4 |
| 7 |
点评:本题考查由三视图求几何体的表面积与离散型随机变量的分布列和期望,此题属于基础题,是近几年高考考查的热点之一.

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
 (文)如图所示,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的全面积为
(文)如图所示,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的全面积为