题目内容
已知点P是曲线y=x3+2x+1上的一点，过点P与此曲线的相切的直线l平行于直线y=2x-3，则切线l的方程是（ ）
A、y=-
| ||
| B、y=2x+1 | ||
| C、y=2x | ||
| D、y=2x+1或y=2x |
分析：由导数的几何意义即可求解．
解答：解：设P点坐标为（x0，y0）
y=x3+2x+1，则y′=3x2+2，
∴3x02+2=2
∴x0=0
∴P点坐标为（0，1）
∴l的方程为：y=2x+1
故选B．
y=x3+2x+1，则y′=3x2+2，
∴3x02+2=2
∴x0=0
∴P点坐标为（0，1）
∴l的方程为：y=2x+1
故选B．
点评：在对导数知识的考查中，导数的几何意义在高考中是经常出现的考点．
练习册系列答案
活力课时同步练习册系列答案
相关题目
已知点P是曲线y=lnx上的一个动点，则点P到直线l：y=x+2的距离的最小值为（ ）
A、
| ||||
| B、2 | ||||
C、
| ||||
D、2
|
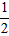x+1