题目内容
已知命题“存在x∈R，|x-a|+|x+2|≤2”是假命题，则实数a的取值范围是
a＜-4或a＞0
a＜-4或a＞0
．分析：由|x-a|+|x+2|≤2的几何意义可求得a的取值范围，取其集合的补集就是所求．
解答：解：由绝对值的几何意义可得，|x-a|+|x+2|≤2是指数轴上的数x到数a和数-2的距离之和小于或等于2，由图可得：
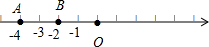
即当数a对应的点位于AO之间时，存在x∈R，|x-a|+|x+2|≤2，
∴-4≤a≤0．
∴“存在x∈R，|x-a|+|x+2|≤2”是假命题，实数a的取值范围是：a＜-4或a＞0．
故答案为：a＜-4或a＞0．
即当数a对应的点位于AO之间时，存在x∈R，|x-a|+|x+2|≤2，
∴-4≤a≤0．
∴“存在x∈R，|x-a|+|x+2|≤2”是假命题，实数a的取值范围是：a＜-4或a＞0．
故答案为：a＜-4或a＞0．
点评：本题考查绝对值不等式，理解|x-a|+|x+2|≤2的几何意义是解题的关键，也是难点，属于中档题．
练习册系列答案
智能训练练测考系列答案
相关题目