题目内容
设计一种正四棱柱形冰箱,它有一个冷冻室和一个冷藏室,冷藏室用两层隔板分为三个抽屉,问:如何设计它的外形尺寸,能使得冰箱体积V=0.5(m3)为定值时,它的表面和三层隔板(包括冷冻室的底层)面积之和S值最小.(参考数据:| 3 | 0.2 |
| 3 | 0.5 |
分析:设水箱的底面边长为x(m),则高为
(m),得出S=5x2+4x•
=5x2+
(x>0)
方法1:求出s′=0时的驻点,分区间函数S在(0,
)上递减,在(
+∞)上递增,得到函数的最小值即可;
方法2:利用a+b≥2
当且仅当a=b时取等号的方法求出此时的x值并求出高即可.
| 0.5 |
| x2 |
| 0.5 |
| x2 |
| 2 |
| x |
方法1:求出s′=0时的驻点,分区间函数S在(0,
| 3 | 0.2 |
| 3 | 0.2, |
方法2:利用a+b≥2
| ab |
解答:解:设水箱的底面边长为x(m),则高为
(m),S=5x2+4x•
=5x2+
(x>0)
法1:S/=10x-
,
由S/>0?x>
,S/<0?0<x<
,
∴函数S在(0,
)上递减,在(
+∞)上递增,
∴x=
≈0.58时,S有最小值,此时
≈1.49
法2:S=5x2+
+
≥3•
=3
(当且仅当5x2=
即x=
≈0.58时,取等号)
∴x=
≈0.58时,S有最小值3
,此时
≈1.49
答:冰箱底面正方形边长为0.58m,高度为1.49m时,它的表面和三层隔板(包括冷冻室的底层)面积之和S值最小.
| 0.5 |
| x2 |
| 0.5 |
| x2 |
| 2 |
| x |
法1:S/=10x-
| 2 |
| x2 |
由S/>0?x>
| 3 | 0.2 |
| 3 | 0.2 |
∴函数S在(0,
| 3 | 0.2 |
| 3 | 0.2, |
∴x=
| 3 | 0.2 |
| 0.5 |
| x2 |
法2:S=5x2+
| 1 |
| x |
| 1 |
| x |
| 3 | 5x2•
| ||||
| 3 | 5 |
| 1 |
| x2 |
| 3 | 0.2 |
∴x=
| 3 | 0.2 |
| 3 | 5 |
| 0.5 |
| x2 |
答:冰箱底面正方形边长为0.58m,高度为1.49m时,它的表面和三层隔板(包括冷冻室的底层)面积之和S值最小.
点评:考查学生根据实际问题选择函数类型的能力,以及会用导数求闭区间上函数的最值和利用公式a+b≥2
当且仅当a=b时取等号的方法求函数最值的能力.
| ab |

练习册系列答案
相关题目
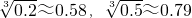 ,0.582=0.3364,0.792=0.6241)
,0.582=0.3364,0.792=0.6241)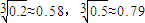 ,0.582=0.3364,0.792=0.6241)
,0.582=0.3364,0.792=0.6241)