题目内容
如图,BC是半圆O的直径,点D是半圆上一点,过点D作⊙O切线AD,BA⊥DA于点A,BA交半圆于点E.已知BC=10,AD=4.那么直线CE与以点O为圆心, 为半径的圆的位置关系是
为半径的圆的位置关系是
- A.相离
- B.相交
- C.相切
- D.不确定
A
分析:要判断直线CE与以点O为圆心, 为半径的圆的位置关系,只需求得圆心到直线的距离,连接OD交CE于F,根据切线的性质,得到要求的距离即是OF,且发现四边形AEFD是矩形.再根据矩形的性质以及垂径定理和勾股定理,即可求解.
为半径的圆的位置关系,只需求得圆心到直线的距离,连接OD交CE于F,根据切线的性质,得到要求的距离即是OF,且发现四边形AEFD是矩形.再根据矩形的性质以及垂径定理和勾股定理,即可求解.
若d<r,则直线与圆相交;若d=r,则直线于圆相切;若d>r,则直线与圆相离.
解答: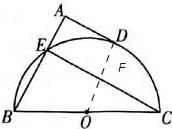 解:连接OD交CE于F,则OD⊥AD.
解:连接OD交CE于F,则OD⊥AD.
又BA⊥DA,
∴OD∥AB.
∵OB=OC,
∴CF=EF,
∴OD⊥CE,
则四边形AEFD是矩形,得EF=AD=4.
连接OE.
在直角三角形OEF中,根据勾股定理得OF= =3>
=3> ,
,
即圆心O到CE的距离大于圆的半径,则直线和圆相离.
故选A.
点评:连接过切点的半径是圆中一条常见的辅助线.此题综合运用了切线的性质、平行线等分线段定理、垂径定理的推论以及勾股定理.
分析:要判断直线CE与以点O为圆心,
 为半径的圆的位置关系,只需求得圆心到直线的距离,连接OD交CE于F,根据切线的性质,得到要求的距离即是OF,且发现四边形AEFD是矩形.再根据矩形的性质以及垂径定理和勾股定理,即可求解.
为半径的圆的位置关系,只需求得圆心到直线的距离,连接OD交CE于F,根据切线的性质,得到要求的距离即是OF,且发现四边形AEFD是矩形.再根据矩形的性质以及垂径定理和勾股定理,即可求解.若d<r,则直线与圆相交;若d=r,则直线于圆相切;若d>r,则直线与圆相离.
解答:
 解:连接OD交CE于F,则OD⊥AD.
解:连接OD交CE于F,则OD⊥AD.又BA⊥DA,
∴OD∥AB.
∵OB=OC,
∴CF=EF,
∴OD⊥CE,
则四边形AEFD是矩形,得EF=AD=4.
连接OE.
在直角三角形OEF中,根据勾股定理得OF=
 =3>
=3> ,
,即圆心O到CE的距离大于圆的半径,则直线和圆相离.
故选A.
点评:连接过切点的半径是圆中一条常见的辅助线.此题综合运用了切线的性质、平行线等分线段定理、垂径定理的推论以及勾股定理.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
如图,BC是半圆O的直径,点D是半圆上一点,过点D作⊙O切线AD,BA⊥DA于点A,BA交半圆于点E.已知BC=10,AD=4.那么直线CE与以点O为圆心,
为半径的圆的位置关系是 ( )
| 5 |
| 2 |
| A、相离 | B、相交 | C、相切 | D、不确定 |
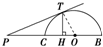
如图,P是半圆O的直径BC延长线上一点,PT切半圆于点T,TH⊥BC于H,若PT=1,PB+PC=2a,则PH=( )

A、
| ||
B、
| ||
C、
| ||
D、
|
 (2012•江苏一模)选做题
(2012•江苏一模)选做题 为半径的圆的位置关系是 ( )
为半径的圆的位置关系是 ( )