题目内容
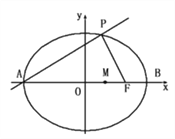
【题目】过曲线![]() 的左焦点
的左焦点![]() 作曲线
作曲线![]() 的切线,设切点为
的切线,设切点为![]() ,延长
,延长![]() 交曲线
交曲线![]() 于点
于点![]() ,其中
,其中![]() ,
,![]() 有一个共同的焦点,若
有一个共同的焦点,若![]() ,则曲线
,则曲线![]() 的离心率为( )
的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
设双曲线的右焦点的坐标为![]() ,利用
,利用![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点,可得
的中点,可得![]() 为
为![]() 的中位线,从而可求
的中位线,从而可求![]() ,再设
,再设![]() ,过点
,过点![]() 作
作![]() 轴的垂线,由勾股定理得出关于
轴的垂线,由勾股定理得出关于![]() 的关系式,最后即可求得离心率.
的关系式,最后即可求得离心率.
设双曲线的右焦点为![]() ,则
,则![]() 的坐标为
的坐标为![]() .
.
因为曲线![]() 与
与![]() 有一个共同的焦点,所以曲线
有一个共同的焦点,所以曲线![]() 的方程为
的方程为![]() .
.
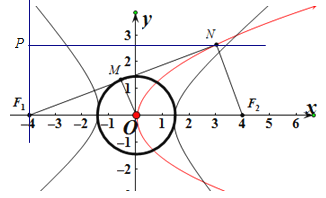
因为![]() ,
,
所以![]() ,
,
所以![]() 为
为![]() 的中点,
的中点,
因为O为![]() 的中点,
的中点,
所以OM为![]() 的中位线,
的中位线,
所以OM∥![]() .
.
因为|OM|=a,所以![]() .
.
又![]() ,
,![]() ,
,
所以![]() .
.
设N(x,y),则由抛物线的定义可得![]() ,
,
所以![]() .
.
过点F1作x轴的垂线,点N到该垂线的距离为![]() ,
,
在![]() 中,由勾股定理得
中,由勾股定理得![]() ,
,
即![]() ,
,
所以![]() ,
,
整理得![]() ,解得
,解得![]() .
.
故选A.

 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案【题目】“海之旅”表演队在一海滨区域进行集训,该海滨区域的海浪高度![]() (米)随着时刻
(米)随着时刻![]() 而周期性变化.为了了解变化规律,该团队观察若干天后,得到每天各时刻
而周期性变化.为了了解变化规律,该团队观察若干天后,得到每天各时刻![]() 的浪高数据的平均值如下表:
的浪高数据的平均值如下表:
| 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| 1.0 | 1.4 | 1.0 | 0.6 | 1.0 | 1.4 | 0.9 | 0.6 | 1.0 |
(1)从![]() 中选择一个合适的函数模型,并求出函数解析式;
中选择一个合适的函数模型,并求出函数解析式;
(2)如果确定当浪高不低于0.8米时才进行训练,试安排白天内恰当的训练时间段.
【题目】某车站在春运期间为了了解旅客购票情况,随机调查了100名旅客从开始在售票窗口排队到购到车票所用的时间![]() (以下简称为购票用时,单位为min),下面是这次调查统计分析得到的频率分布表和频率分布直方图.
(以下简称为购票用时,单位为min),下面是这次调查统计分析得到的频率分布表和频率分布直方图.
频率 | 分组 | 频数 |
| 10 | 0.10 |
| 10 | ② |
| ① | 0.50 |
| 30 | 0.30 |
合计 | 100 | 1.00 |
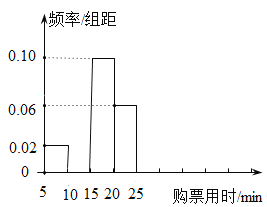
解答下列问题:
(1)在表中填写出缺失的数据并补全频率分布直方图;
(2)估计旅客购票用时的平均数.
【题目】2019年某地遭遇严重干旱,某乡计划向上级申请支援,为上报需水量,乡长事先抽样调查100户村民的月均用水量,得到这100户村民月均用水量(单位:t)的频率分布表如下:
月均用水量分组 | 频数 | 频率 |
| 12 | |
| ||
| 40 | |
| 0.18 | |
| 6 | |
合计 | 100 | 1.00 |
(1)请完成该频率分布表,并画出相对应的频率分布直方图.
(2)样本的中位数是多少?
(3)已知上级将按每户月均用水量向该乡调水,若该乡共有1200户,请估计上级支援该乡的月调水量是多少吨.
【题目】当前,以“立德树人”为目标的课程改革正在有序推进.高中联招对初三毕业学生进行体育测试,是激发学生、家长和学校积极开展体育活动,保证学生健康成长的有效措施.程度2019年初中毕业生升学体育考试规定,考生必须参加立定跳远、掷实心球、1分钟跳绳三项测试,三项考试满分50分,其中立定跳远15分,掷实心球15分,1分钟跳绳20分.某学校在初三上期开始时要掌握全年级学生每分钟跳绳的情况,随机抽取了100名学生进行测试,得到下边频率分布直方图,且规定计分规则如下表:
每分钟跳绳个数 |
|
|
|
|
得分 | 17 | 18 | 19 | 20 |
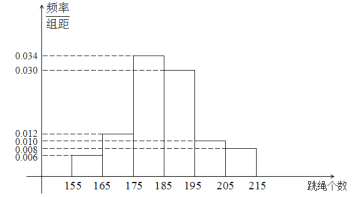
(Ⅰ)现从样本的100名学生中,任意选取2人,求两人得分之和不大于35分的概率;;
(Ⅱ)若该校初三年级所有学生的跳绳个数![]() 服从正态分布
服从正态分布![]() ,用样本数据的平均值和方差估计总体的期望和方差,已知样本方差
,用样本数据的平均值和方差估计总体的期望和方差,已知样本方差![]() (各组数据用中点值代替).根据往年经验,该校初三年级学生经过一年的训练,正式测试时每人每分钟跳绳个数都有明显进步,假设今年正式测试时每人每分钟跳绳个数比初三上学期开始时个数增加10个,现利用所得正态分布模型:
(各组数据用中点值代替).根据往年经验,该校初三年级学生经过一年的训练,正式测试时每人每分钟跳绳个数都有明显进步,假设今年正式测试时每人每分钟跳绳个数比初三上学期开始时个数增加10个,现利用所得正态分布模型:
![]() 预计全年级恰有2000名学生,正式测试每分钟跳182个以上的人数;(结果四舍五入到整数)
预计全年级恰有2000名学生,正式测试每分钟跳182个以上的人数;(结果四舍五入到整数)
![]() 若在全年级所有学生中任意选取3人,记正式测试时每分钟跳195以上的人数为ξ,求随机变量的分布列和期望.
若在全年级所有学生中任意选取3人,记正式测试时每分钟跳195以上的人数为ξ,求随机变量的分布列和期望.
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.