题目内容
在数列
中，
，
，
．
（Ⅰ）证明数列
是等比数列；
（Ⅱ）求数列的前
项和
；
（Ⅲ）证明不等式
，对任意皆成立．
本小题以数列的递推关系式为载体，主要考查等比数列的概念、等比数列的通项公式及前
项和公式、不等式的证明等基础知识，考查运算能力和推理论证能力．
（Ⅰ）证明：由题设
，得
，
．
又
，所以数列
是首项为
，且公比为
的等比数列．
（Ⅱ）解：由（Ⅰ）可知
，于是数列
的通项公式为
．
所以数列的前项和
．
（Ⅲ）证明：对任意的，
．
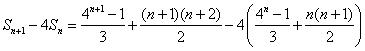
所以不等式
，对任意皆成立．
练习册系列答案
相关题目