题目内容
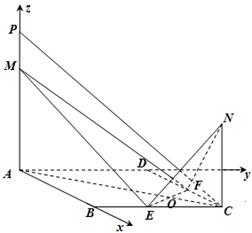
如图,已知 ,
,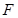 分别是正方形
分别是正方形 边
边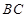 、
、 的中点,
的中点, 与
与 交于点
交于点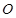 ,
,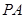 、
、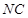 都垂直于平面
都垂直于平面 ,且
,且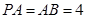 ,
,
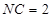 ,
,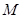 是线段
是线段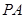 上一动点.
上一动点.
(Ⅰ)求证:平面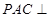 平面
平面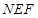 ;
;
(Ⅱ)若 平面
平面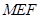 ,试求
,试求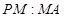 的值;
的值;
(Ⅲ)当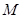 是
是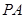 中点时,求二面角
中点时,求二面角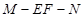 的余弦值.
的余弦值.
【答案】
法1:(Ⅰ)连结 ,
,
∵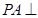 平面
平面 ,
, 平面
平面 ,∴
,∴ ,
,
又∵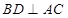 ,
,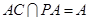 ,
,
∴ 平面
平面 ,
,
又∵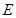 ,
, 分别是
分别是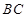 、
、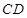 的中点,∴
的中点,∴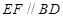 ,
,
∴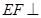 平面
平面 ,又
,又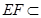 平面
平面 ,
,
∴平面 平面
平面 ;
;
(Ⅱ)连结 ,
,
∵ 平面
平面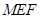 ,平面
,平面 平面
平面 ,
,
∴
 ,
,
∴ ,故
,故
(Ⅲ)∵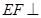 平面
平面 ,
, 平面
平面 ,∴
,∴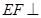
 ,
,
在等腰三角形 中,点
中,点 为
为 的中点,∴
的中点,∴ ,
,
∴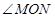 为所求二面角
为所求二面角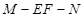 的平面角,
的平面角,
∵点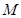 是
是 的中点,∴
的中点,∴ ,
,
所以在矩形 中,可求得
中,可求得 ,
, ,
, ,
,
在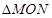 中,由余弦定理可求得
中,由余弦定理可求得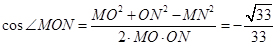 ,
,
∴二面角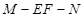 的余弦值为
的余弦值为 .
.
法2:(Ⅰ)同法1;
(Ⅱ)建立如图所示的直角坐标系,则 ,
, ,
, ,
,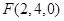 ,
,
∴ ,
,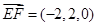 ,
,
设点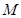 的坐标为
的坐标为 ,平面
,平面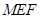 的法向量为
的法向量为 ,则
,则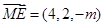 ,
,
所以 ,即
,即 ,令
,令 ,则
,则 ,
, ,
,
故 ,
,
∵ 平面
平面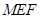 ,∴
,∴ ,即
,即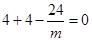 ,解得
,解得 ,
,
故 ,即点
,即点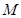 为线段
为线段 上靠近
上靠近 的四等分点;故
的四等分点;故
(Ⅲ)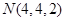 ,则
,则 ,
,
设平面 的法向量为
的法向量为 ,
,
则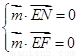 ,即
,即 ,令
,令 ,
,
则 ,
, ,即
,即 ,
,
当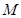 是
是 中点时,
中点时,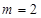 ,则
,则 ,
,
∴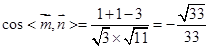 ,
,
∴二面角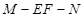 的余弦值为
的余弦值为 .
.
【解析】略

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
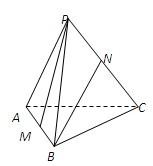 如图,已知正四面体P-ABC中,棱AB、PC的中点分别是M、N.
如图,已知正四面体P-ABC中,棱AB、PC的中点分别是M、N. 如图,已知P、O分别是正四棱柱ABCD-A1B1C1D1上、下底面的中心,E是AB的中点,AB=kAA1,其中k为非零实数,
如图,已知P、O分别是正四棱柱ABCD-A1B1C1D1上、下底面的中心,E是AB的中点,AB=kAA1,其中k为非零实数,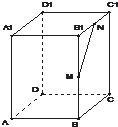 (2013•浦东新区二模)如图,已知正四棱柱ABCD-A1B1C1D1的底面边长是2,体积是16,M,N分别是棱BB1、B1C1的中点.
(2013•浦东新区二模)如图,已知正四棱柱ABCD-A1B1C1D1的底面边长是2,体积是16,M,N分别是棱BB1、B1C1的中点. (2006•崇文区二模)如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长为
(2006•崇文区二模)如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长为  如图,已知正三棱柱ABC-A1B1C1的,底面边长是侧棱长2倍,D、E分别是AC、A1C1的中点;
如图,已知正三棱柱ABC-A1B1C1的,底面边长是侧棱长2倍,D、E分别是AC、A1C1的中点;