题目内容
如图,在平面四边形ABCD中,已知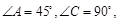
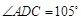 ,
,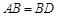 ,现将四边形ABCD沿BD折起,使平面ABD
,现将四边形ABCD沿BD折起,使平面ABD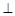 平面BDC,设点F为棱AD的中点.
平面BDC,设点F为棱AD的中点.

(1)求证:DC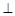 平面ABC;
平面ABC;
(2)求直线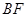 与平面ACD所成角的余弦值.
与平面ACD所成角的余弦值.
(1)见解析;(2)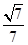 .
.
解析试题分析:(1)要证DC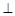 平面ABC,则需证DC垂直平面ABC内的两条相交直线,需证AB⊥CD,CD⊥BC,可得结论;(2)求直线与面所成的角,需过直线上一点(异于与面的交点)向面作垂线,此题根据已知条件在面ABC内过点B向AC作垂线BE,再证BE与面ADC垂直,即可找出直线BF与面ACD所成的角,最后在角所在的三角形中求解.
平面ABC,则需证DC垂直平面ABC内的两条相交直线,需证AB⊥CD,CD⊥BC,可得结论;(2)求直线与面所成的角,需过直线上一点(异于与面的交点)向面作垂线,此题根据已知条件在面ABC内过点B向AC作垂线BE,再证BE与面ADC垂直,即可找出直线BF与面ACD所成的角,最后在角所在的三角形中求解.
试题解析:(1)证明:在图甲中∵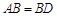 且
且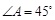 ∴
∴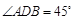 ,
,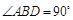 ,即
,即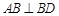
在图乙中,∵平面ABD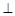 平面BDC , 且平面ABD
平面BDC , 且平面ABD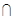 平面BDC=BD,∴AB⊥底面BDC,∴AB⊥CD.
平面BDC=BD,∴AB⊥底面BDC,∴AB⊥CD.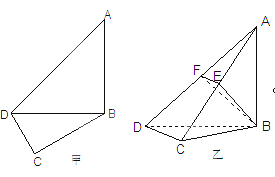
又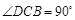 ,∴DC⊥BC,且
,∴DC⊥BC,且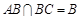 ∴DC
∴DC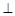 平面ABC. 7分
平面ABC. 7分
(2)解:作BE⊥AC,垂足为E,
由(1)知平面ABC⊥平面ACD,又平面ABC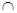 平面ACD=AC,∴BF⊥平面ADC,
平面ACD=AC,∴BF⊥平面ADC,
∴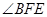 即为直线
即为直线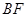 与平面ACD所成角
与平面ACD所成角
设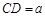 得AB=
得AB=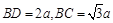 ,AC=
,AC=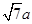
∴ ,
,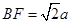 ,
,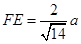 ∴
∴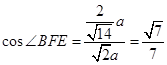 ,
,
∴直线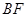 与平面ACD所成角的余弦值为
与平面ACD所成角的余弦值为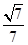 . ..14分
. ..14分
考点:1、线面垂直的判定定理;2、直线与面所成角的作法及求发.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
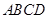 中,
中,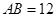 ,
,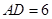 ,
,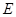 、
、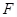 分别为
分别为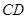 、
、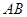 边上的点,且
边上的点,且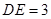 ,
,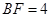 ,将
,将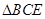 沿
沿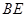 折起至
折起至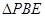 位置(如图2所示),连结
位置(如图2所示),连结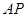 、
、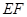 、
、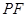 ,其中
,其中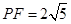 .
.
 平面
平面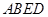 ;
;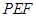 所成角的正弦值.
所成角的正弦值.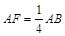 .
.
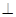 面ABEF,且DA=1,AB//EF,
面ABEF,且DA=1,AB//EF,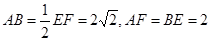 ,P、Q、M分别为AE、BD、EF的中点.
,P、Q、M分别为AE、BD、EF的中点.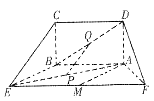

 中,已知
中,已知 是棱
是棱 的中点.
的中点.
 平面
平面 ,
, ∥平面
∥平面 ;
; 底面ABCD,SA=AD,点M是SD的中点,AN
底面ABCD,SA=AD,点M是SD的中点,AN
 底面ABCD,PD
底面ABCD,PD ADC-900,AB=AD=PD=1.CD=2.
ADC-900,AB=AD=PD=1.CD=2.
 ,试确定
,试确定 的值,使得二面角
的值,使得二面角 .
.