题目内容
一个正方体的棱长为2,将8个直径均为1的球放进去之后.正中央空间能放下的最大的球的直径为
-1
-1.
| 3 |
| 3 |
分析:说明8个小球的位置关系,利用正方体的中心与8个小球的中心的距离关系推出结果即可.
解答:解:将原正方体分为8个棱长为1的小正方体,则每个小正方体都有一个直径为1的球,
原正方体的中心为每个小正方体的中心到原正方体的中心的距离为:
,
又小正方体的中心到球表面的距离为:
,
所以原正方体的中心到球的表面的最远距离为:
,
所以正中央空间能放下的最大的球的直径为:
-1.
故答案为:
-1.
原正方体的中心为每个小正方体的中心到原正方体的中心的距离为:
| ||
| 2 |
又小正方体的中心到球表面的距离为:
| 1 |
| 2 |
所以原正方体的中心到球的表面的最远距离为:
| ||
| 2 |
所以正中央空间能放下的最大的球的直径为:
| 3 |
故答案为:
| 3 |
点评:本题考查球的位置关系,考查空间想象能力逻辑推理能力.

练习册系列答案
相关题目
已知一个正方体的棱长为
2,以相对两个面的中心连线为轴,钻一个直径为1的圆柱形孔,这个几何体的表面积为[
]|
A .24-2p |
B .24+2p |
|
C .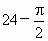 |
D .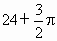 |