题目内容
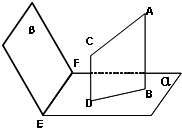 如图,平面αIβ=EF,AB⊥α,CD⊥α,垂足分别是B、D,如果增加一个条件,就能推出BD⊥EF,现有下面4个条件:
如图,平面αIβ=EF,AB⊥α,CD⊥α,垂足分别是B、D,如果增加一个条件,就能推出BD⊥EF,现有下面4个条件:①AC⊥β;
②AC与α,β所成的角相等;
③平面ABC⊥β;
④AC与BD在β内的射影在同一条直线上.
其中能成为增加条件的是
①③④
①③④
.(把你认为正确的条件的序号都填上)分析:要增加一个条件,推出BD⊥EF,由AB⊥α,CD⊥α,则平面ABDC与EF垂直,需要加一个条件能够使得线与面垂直,把几个选项逐个分析,得到结论.
解答:解:要增加一个条件,推出BD⊥EF,
∵AB⊥α,CD⊥α,∴平面ABDC与EF垂直,
∴需要加一个条件能够使得线与面垂直,
①通过线面垂直得到线线垂直,使得EF垂直于平面ABDC,所以①可以成为增加的条件;
②AC与α,β所成的角相等,AC与EF 不一定,可以是相交、可以是平行、也可能垂直,所以EF与平面ACDB不垂直,所以就推不出EF与BD垂直,所以②不可以成为增加的条件;
③因为平面ABC⊥β,平面ABDC⊥α,α∩β=EF,所以EFEF⊥平面ACBD,所以③可以成为增加的条件;
④因为CD⊥α且EF?α所以EF⊥CD,所以EF与CD在β内的射影垂直,
因为AC与CD在β内的射影在同一条直线上,所以EF⊥AC
因为AC∩CD=C,AC?平面ACBD,CD?平面ACBD,所以EF⊥平面ACBD,所以④可以成为增加的条件.
故答案为:①③④
∵AB⊥α,CD⊥α,∴平面ABDC与EF垂直,
∴需要加一个条件能够使得线与面垂直,
①通过线面垂直得到线线垂直,使得EF垂直于平面ABDC,所以①可以成为增加的条件;
②AC与α,β所成的角相等,AC与EF 不一定,可以是相交、可以是平行、也可能垂直,所以EF与平面ACDB不垂直,所以就推不出EF与BD垂直,所以②不可以成为增加的条件;
③因为平面ABC⊥β,平面ABDC⊥α,α∩β=EF,所以EFEF⊥平面ACBD,所以③可以成为增加的条件;
④因为CD⊥α且EF?α所以EF⊥CD,所以EF与CD在β内的射影垂直,
因为AC与CD在β内的射影在同一条直线上,所以EF⊥AC
因为AC∩CD=C,AC?平面ACBD,CD?平面ACBD,所以EF⊥平面ACBD,所以④可以成为增加的条件.
故答案为:①③④
点评:本题是个开放性的命题,解决此类问题关键是熟记相关的平行与垂直的定理,准确把握定理中的条件.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
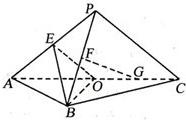 如图,平面PAC⊥平面ABC,△ABC是以AC为斜边的等腰直角三角形,E、F、O分别为PA,PB,AC的中点,AC=16,PA=PC=10.
如图,平面PAC⊥平面ABC,△ABC是以AC为斜边的等腰直角三角形,E、F、O分别为PA,PB,AC的中点,AC=16,PA=PC=10. 如图,平面EAD⊥平面ABFD,△AED为正三角形,四边形ABFD为直角梯形,且∠BAD=90°,
如图,平面EAD⊥平面ABFD,△AED为正三角形,四边形ABFD为直角梯形,且∠BAD=90°, 如图,四棱锥 E-ABCD中,EA⊥平面ABCD,AB⊥AD,AB∥DC,AD=AE=CD=2AB,M是EC的中点.
如图,四棱锥 E-ABCD中,EA⊥平面ABCD,AB⊥AD,AB∥DC,AD=AE=CD=2AB,M是EC的中点. 中,D,E,F分别是AB,AC和BC边的中点,
中,D,E,F分别是AB,AC和BC边的中点, ,现将
,现将

 DE?证明你的结论.
DE?证明你的结论.