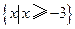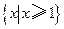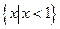题目内容
(CUA)∪B, A∩(CUB).
A∩B={x|x＞3或x＜1} A∪B={x|x＞2或x≤1}
(
UA)∪B={x|x≥2或x≤1}=U. A∩(UB)= 
(
UA)∪B={x|x≥2或x≤1}=U. A∩(UB)= ∵U={x|x2-3x+2≥0}={x|(x-2)(x-1)≥0}={x|x≥2或x≤1}, A={x||x-2|＞1}
={x|x-2＞1或x-2＜-1}={x|x＞3或x＜1},
B={x|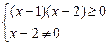
}={x|x＞2或x≤1}.由图(1)可知,A∩B={x|x＞3或x＜1},
A∪B={x|x＞2或x≤1}.
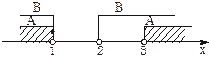
图(1)
由图(2)可知UA={x|2≤x≤3或x="1}, " 易知UB={x|x=2}.
图(2)
由图(3)可知,(UA)∪B={x|x≥2或x≤1}=U.
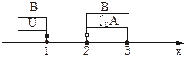
图(3)
由图(4)可知,A∩(UB)= .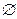
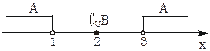
={x|x-2＞1或x-2＜-1}={x|x＞3或x＜1},
B={x|
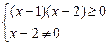}={x|x＞2或x≤1}.由图(1)可知,A∩B={x|x＞3或x＜1},A∪B={x|x＞2或x≤1}.
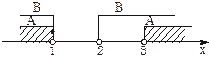
图(1)
由图(2)可知
UA={x|2≤x≤3或x="1}, " 易知UB={x|x=2}.图(2)
由图(3)可知,(
UA)∪B={x|x≥2或x≤1}=U.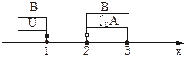图(3)
由图(4)可知,A∩(
UB)= .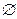
练习册系列答案
相关题目
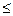5｝，B=｛x︱x2+x
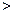2｝，求A
(
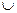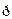uB).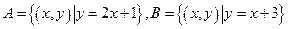
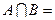
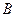
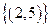
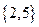
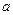为元素的集合B；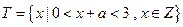
UA=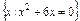
，B={x|x2+3（a+1）x+a2-1=0}，且A∪B=A，求实数a的取值范围.
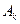的最小元素为
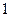，最大元素为
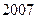，并且各元素可以从小到大排成一个公差为
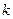的等差数列，则并集
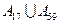中的元素个数为（ ）．
、
、
； 
、
； 
、
.
，
（ ）
，
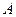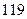
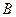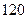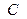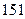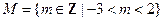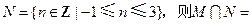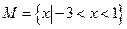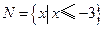，则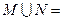
（ ）
