题目内容
有下面四个判断，其中正确的个数是（ ）①命题：“设a、b∈R，若a+b≠6，则a≠3或b≠3”是一个真命题
②若“p或q”为真命题，则p、q均为真命题
③命题“?a、b∈R，a2+b2≥2（a-b-1）”的否定是：“?a、b∈R，a2+b2≤2（a-b-1）”
A．0
B．1
C．2
D．3
【答案】分析：写出①的逆否命题，判断逆否命题的真假，即可判断①的正误．
通过复合命题的真假判断②的正误；
利用全称命题的否定，写出其特称命题判断即可．
解答：解：①命题：“设a、b∈R，若a+b≠6，则a≠3或b≠3”的逆否命题为：“若a=3且b=3，则a+b=6”是一个真命题，
所以①是真命题；
②若“p或q”为真命题，一真即真，所以p、q均为真命题说法不正确；
③命题“?a、b∈R，a2+b2≥2（a-b-1）”的否定是：“?a、b∈R，a2+b2≤2（a-b-1）”不满足全称命题的否定是特称命题，所以不正确；
正确命题的个数是1个．
故选B．
点评：本题考查命题的否定，四种命题的逆否关系，复合命题真假的判断，基本知识的应用．
通过复合命题的真假判断②的正误；
利用全称命题的否定，写出其特称命题判断即可．
解答：解：①命题：“设a、b∈R，若a+b≠6，则a≠3或b≠3”的逆否命题为：“若a=3且b=3，则a+b=6”是一个真命题，
所以①是真命题；
②若“p或q”为真命题，一真即真，所以p、q均为真命题说法不正确；
③命题“?a、b∈R，a2+b2≥2（a-b-1）”的否定是：“?a、b∈R，a2+b2≤2（a-b-1）”不满足全称命题的否定是特称命题，所以不正确；
正确命题的个数是1个．
故选B．
点评：本题考查命题的否定，四种命题的逆否关系，复合命题真假的判断，基本知识的应用．
练习册系列答案
相关题目
、
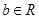，若
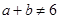，则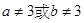
”是一个真命题
、
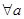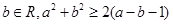”的否定是：“
、
”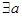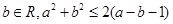