题目内容
函数 在一个周期内的图象如右,则此函数的解析式为( )
在一个周期内的图象如右,则此函数的解析式为( )
A. | B. |
C. | D. |
A
解析试题分析:由图象知,函数的振幅为2,即A=2, ,∴
,∴ ,把点
,把点 代入
代入 得
得 ,∴
,∴ ,∴
,∴ ,∴函数的解析式为
,∴函数的解析式为 ,故选A
,故选A
考点:本题考查了三角函数解析式的求法
点评:根据图象写出解析式,一般通过图象的最高或最低点先求得函数的周期和振幅,再根据图象上的已知求得初相,进行可求得函数的解析式

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
为了得到函数 的图象,可以将函数
的图象,可以将函数 的图象( )
的图象( )
A.向右平移 个单位长度 个单位长度 | B.向右平移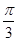 个单位长度 个单位长度 |
C.向左平移 个单位长度 个单位长度 | D.向左平移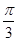 个单位长度 个单位长度 |
已知 ,则
,则
A. | B. | C. | D. |
函数 (
(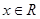 )的部分图像如图所示,如果,且
)的部分图像如图所示,如果,且 ,则
,则 ( )
( )
A. | B. | C. | D.1 |
若 是第四象限角,
是第四象限角, ,则
,则
A.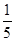 | B.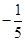 | C. | D. |
 的值是( )
的值是( )
A. | B. | C. | D. |
关于函数 的四个结论:
的四个结论:
P1:最大值为 ; P2:最小正周期为
; P2:最小正周期为 ;
;
P3:单调递增区间为 Z;
Z;
P4:图象的对称中心为 Z .其中正确的有( )
Z .其中正确的有( )
| A.1 个 | B.2个 | C.3个 | D.4个 |
 的最大值为
的最大值为
A. | B. | C. | D. |

 在区间
在区间 上单调递减,且函数值从1减小到
上单调递减,且函数值从1减小到 ,那么此函数图象与
,那么此函数图象与 轴交点的纵坐标为( )
轴交点的纵坐标为( )


