题目内容
(12分)抛物线的顶点在坐标原点,焦点在 轴的负半轴上,过点
轴的负半轴上,过点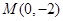 作直线
作直线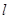 与抛物线交于A,B两点,且满足
与抛物线交于A,B两点,且满足 ,
,
(1)求抛物线的方程
(2)当抛物线上的一动点P从A运动到B时,求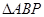 面积的的最大值.
面积的的最大值.
(1) 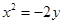 (2)
(2) 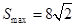
解析试题分析:(1)设直线的方程为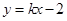 与抛物线
与抛物线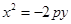 联立消去
联立消去 得
得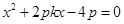
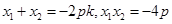 又
又

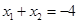 ,
,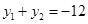 得
得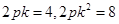 解得
解得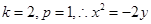
(2)底确定当高最大时面积最大,此时的高就是平行于AB且与抛物线相切的直线和直线AB间的距离设直线方程为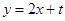 利用相切条件即
利用相切条件即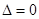 得
得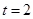
于是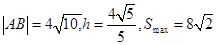
考点:直线和抛物线的位置关系及数形结合法求最值
点评:直线和圆锥曲线的位置关系通常联立方程利用韦达定理

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
 、
、 分别是圆
分别是圆 和椭圆
和椭圆 的弦,且弦的端点在
的弦,且弦的端点在 轴的异侧,端点
轴的异侧,端点 与
与 、
、 与
与 的横坐标分别相等,纵坐标分别同号.
的横坐标分别相等,纵坐标分别同号.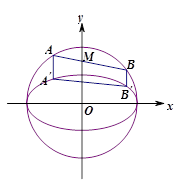
 ,且弦
,且弦 ,求直线
,求直线 ,试探究弦
,试探究弦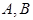 是椭圆
是椭圆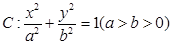 的左、右顶点,椭圆
的左、右顶点,椭圆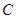 的离心率为
的离心率为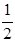 ,右准线
,右准线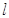 的方程为
的方程为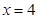 .
.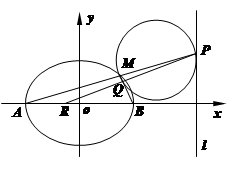
 是椭圆
是椭圆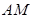 交
交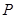 ,以
,以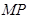 为直径的圆记为
为直径的圆记为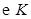 .
. 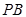 所得的弦长;
所得的弦长;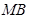 交于点
交于点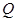 ,试证明:直线
,试证明:直线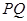 与
与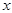 轴的交点
轴的交点 为定点,并求该定点的坐标.
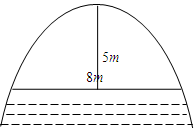
为定点,并求该定点的坐标.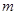 时,水面宽为8
时,水面宽为8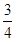
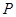 是圆
是圆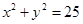 上的动点,点D是
上的动点,点D是 轴上的投影,M为
轴上的投影,M为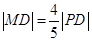
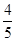 的直线被C所截线段的长度。
的直线被C所截线段的长度。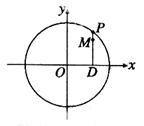
 的右焦点F为
的右焦点F为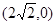 ,G上的点到点F的最大距离为
,G上的点到点F的最大距离为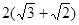 ,斜率为1的直线
,斜率为1的直线 与椭圆G交与
与椭圆G交与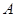 、
、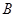 两点,以AB为底边作等腰三角形,顶点为P(-3,2)
两点,以AB为底边作等腰三角形,顶点为P(-3,2)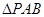 的面积。
的面积。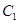 上任意一点M满足
上任意一点M满足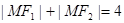 , 其中F
, 其中F (-
(-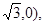 F
F (
(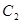 的焦点是直线y=x-1与x轴的交点, 顶点为原点O.
的焦点是直线y=x-1与x轴的交点, 顶点为原点O. 满足条件:①过
满足条件:①过 ;②与
;②与 ,
,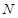 ,且满足
,且满足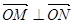 ?若存在,求出直线
?若存在,求出直线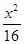
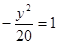 的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,
的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,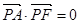
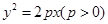 过点A
过点A 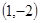
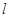 过定点
过定点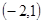 ,斜率为
,斜率为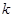 ,当
,当