题目内容
如图,在四棱锥P—ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,PA=AB=4,G为PD的中点,E是AB的中点. 
(Ⅰ)求证:AG∥平面PEC;
(Ⅱ)求点G到平面PEC的距离.
(Ⅰ)详见解析;(Ⅱ)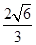
解析试题分析:(Ⅰ)要证明一条直线和一个平面平行,只需在面内找一条直线与之平行,如果找不到,可将这条直线平移到平面内,取 中点
中点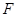 ,连接
,连接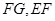 ,则
,则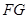 是
是 的中位线,则有
的中位线,则有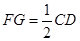 ,
,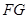 ∥
∥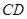 ,又
,又 ∥
∥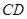 ,
,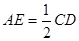 ,∴可证四边形
,∴可证四边形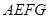 是平行四边形,从而
是平行四边形,从而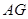 ∥
∥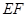 ,可证
,可证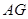 ∥面
∥面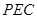 ;
;
(Ⅱ)点到平面的距离指的是点到平面垂线段的长度,如果垂足不好确定,可考虑四面体的等体积转换,由(Ⅰ)知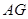 ∥面
∥面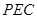 ,∴点
,∴点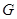 和点
和点 到面
到面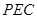 的距离相等,设点
的距离相等,设点 到平面
到平面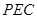 的距离为
的距离为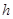
由 ,可求
,可求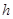 .
.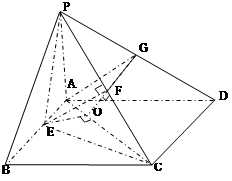
试题解析:(Ⅰ)证明:取PC的中点F,连接GF,则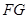 ∥
∥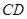 又
又 ∥
∥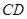 ,且
,且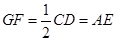
∴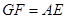 ,
,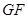 ∥
∥ ,四边形GAEF是平行四边形 ∴
,四边形GAEF是平行四边形 ∴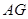 ∥
∥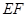 ------4分
------4分
又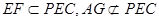 , ∴
, ∴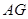 ∥面
∥面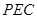 . 6分
. 6分
(Ⅱ)由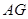 ∥面
∥面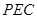 ,知点
,知点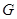 和点
和点 到面
到面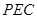 的距离相等,设点
的距离相等,设点 到平面
到平面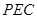 的距离为
的距离为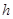 ,
,
∴  , 9分
, 9分
又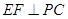 ,
,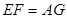
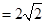 ,
,
∴ 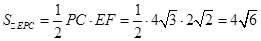 10分
10分
又 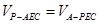 ,∴
,∴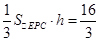 ,
,
即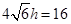 ,
,
∴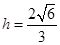 ,∴ G点到平面PEC的距离为
,∴ G点到平面PEC的距离为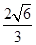 . 12分
. 12分
考点:1、线和面平行的判定;2、点到面的距离.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
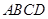 中,
中,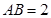 ,
,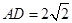 ,
,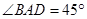 ,以
,以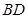 为折线,把
为折线,把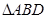 折起,使平面
折起,使平面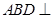 平面
平面 ,连结
,连结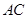 .
.
 ;
; 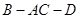 的大小.
的大小.
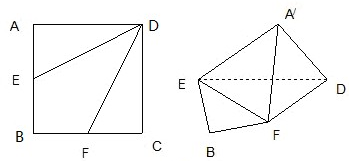
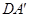 ⊥EF;
⊥EF;
 中,
中,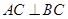 ,点D是AB的中点,
,点D是AB的中点,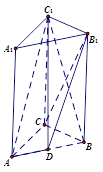
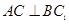 ; (2)
; (2)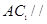 平面
平面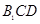
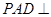 平面
平面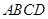 ,
,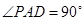 ,且
,且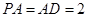 ,
, 、
、 、
、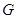 分别是线段
分别是线段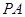 、
、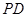 、
、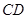 的中点.
的中点.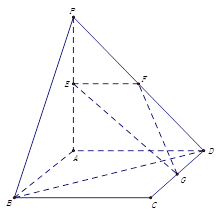
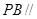 平面
平面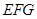 ;
;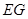 、
、 所成角的余弦值.
所成角的余弦值. ,BC = 6.
,BC = 6.
 中,四边形
中,四边形 是菱形,
是菱形, ,E为PB的中点.
,E为PB的中点.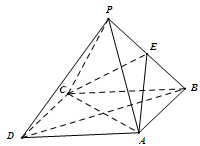
 平面
平面 ;
; 平面
平面 .
. 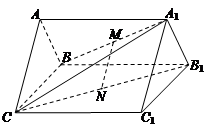
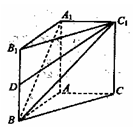
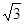 ,BC=2,求二面角A—A1C—B的余弦值的大小
,BC=2,求二面角A—A1C—B的余弦值的大小  中,
中,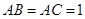 ,
,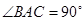 ,异面直线
,异面直线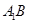 与
与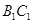 所成
所成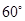 .
.
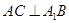 ;
;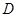 是
是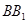 的中点,求
的中点,求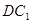 与平面
与平面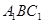 所成角的正弦值.
所成角的正弦值.