题目内容
已知集合A={x|x2-4x-5=0}，B={x|x2=1}，则A∩B=（ ）
| A、{-1} |
| B、{5，-1} |
| C、{1，-1} |
| D、{1.5，-1} |
考点：交集及其运算
专题：集合
分析：利用交集性质求解．
解答：
解：∵A={x|x2-4x-5=0}={-1，5}，
B={x|x2=1}={-1，1}，
∴A∩B={-1}．
故选：A．
B={x|x2=1}={-1，1}，
∴A∩B={-1}．
故选：A．
点评：本题考查交集的求法，是基础题，解题时要认真审题．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
目标函数z=2x+y，变量x，y满足
，则有（ ）
|
| A、zmax=12，zmin=3 | ||
B、zmax=10，zmin=
| ||
| C、zmin=3，z无最大值 | ||
| D、z既无最大值，也无最小值 |
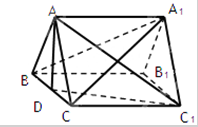如图所示，在三棱柱ABC-A1B1C1中，底面ABC是边长为2的正三角形，侧棱长为3，且侧棱AA1⊥面ABC，点D是BC的中点，求证：平面BB1C1C丄平面ADC1．