题目内容
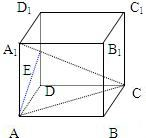 由正方体ABCD-A1B1C1D1的顶点A作这正方体的对角线A1C的垂线,垂足为E,证明A1E:EC=1:2.
由正方体ABCD-A1B1C1D1的顶点A作这正方体的对角线A1C的垂线,垂足为E,证明A1E:EC=1:2.
分析:设正方体的棱长为1,连接AC,求出AC,利用A1E•A1C=AA12,EC•A1C=AC2,可求A1E:EC,进而可证命题.
解答:证明:设正方体的棱长为1,连接AC,则AC=
,
∵为直角△A1AC的斜边A1C上的高,
∴A1E•A1C=AA12,
EC•A1C=AC2,
两式相除,得
=
=
=
,
∴A1E:EC=1:2.
| 2 |
∵为直角△A1AC的斜边A1C上的高,
∴A1E•A1C=AA12,
EC•A1C=AC2,
两式相除,得
| A1E |
| EC |
| AA12 |
| AC2 |
| 1 | ||
(
|
| 1 |
| 2 |
∴A1E:EC=1:2.
点评:本题考查棱柱的结构特征,考查计算能力,逻辑思维能力,是基础题.

练习册系列答案
相关题目
 由正方体ABCD-A1B1C1D1的顶点A作这正方体的对角线A1C的垂线,垂足为E,证明A1E:EC=1:2.
由正方体ABCD-A1B1C1D1的顶点A作这正方体的对角线A1C的垂线,垂足为E,证明A1E:EC=1:2.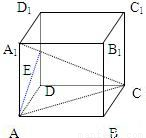 由正方体ABCD-A1B1C1D1的顶点A作这正方体的对角线A1C的垂线,垂足为E,证明A1E:EC=1:2.
由正方体ABCD-A1B1C1D1的顶点A作这正方体的对角线A1C的垂线,垂足为E,证明A1E:EC=1:2.