题目内容
数列
的前n项和．
（1）求证：数列
是等比数列，并求{bn}的通项公式；
（2）如果{bn}对任意
恒成立，求实数k的取值范围．
的前n项和．（1）求证：数列
是等比数列，并求{bn}的通项公式；（2）如果{bn}对任意
恒成立，求实数k的取值范围．（1）证明：对任意n∈N*，都有
，
所以
则数列
成等比数列，首项为
，公比为
所以
，
∴
（2）解：因为
所以
因为不等式
，
化简得
对任意n∈N*恒成立
设
，则
当n≥5，cn+1≤cn，{cn}为单调递减数列，
当1≤n＜5，cn+1＞cn，{cn}为单调递增数列
∵
，
，
∴c4＜c5，
∴n=5时，cn取得最大值
所以，要使
对任意n∈N*恒成立，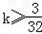
，所以
则数列
成等比数列，首项为，公比为所以
，∴
（2）解：因为
所以
因为不等式
，化简得
对任意n∈N*恒成立设
，则当n≥5，cn+1≤cn，{cn}为单调递减数列，
当1≤n＜5，cn+1＞cn，{cn}为单调递增数列
∵
， ，∴c4＜c5，
∴n=5时，cn取得最大值
所以，要使
对任意n∈N*恒成立，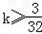
练习册系列答案
相关题目