题目内容
某人进行射击训练,击中目标的概率是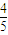 ,且各次射击的结果互不影响.
,且各次射击的结果互不影响.(Ⅰ)假设该人射击5次,求恰有2次击中目标的概率;
(Ⅱ)假设该人每射击5发子弹为一组,一旦命中就停止,并进入下一组练习,否则一直打完5发子弹才能进入下一组练习,求:
①在完成连续两组练习后,恰好共使用了4发子弹的概率;
②一组练习中所使用子弹数ξ的分布列,并求ξ的期望.
【答案】分析:(I)利用独立重复试验的概率公式,即可求射击5次,恰有2次击中目标的概率;
(Ⅱ)①利用独立重复试验的概率公式,可求完成两组练习后,恰好共耗用4发子弹的概率;
②确定ξ可能取值,求出相应的概率,从而可得分布列与期望.
解答:解:(I)设射击5次,恰有2次击中目标的事件为A.
∴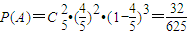 …(4分)
…(4分)
(Ⅱ)①完成两组练习后,恰好共耗用4发子弹的事件为B,则
P(B)=0.8•(1-0.8)2•0.8+(1-0.8)•0.8(1-0.8)•0.8+(1-0.8)2•0.8•08=0.0768.…(8分)
②ξ可能取值为1,2,3,4,5.…(9分)
P(ξ=1)=0.8; P(ζ=2)=(1-0.8)•0.8=0.16;
P(ζ=3)=(1-0.8)2•0.8=0.032;P(ζ=4)=(1-0.8)3•0.8=0.0064;
P(ζ=5)=(1-0.8)4•0.8=0.0016…(11分)
ζ的分布列为
∴Eζ=1×0.8+2×0.16+3×0.032+4×0.0064+5×0.0016=1.2496…(13分)
点评:本题考查独立重复试验的概率,考查离散型随机变量的分布列与期望,解题的关键是求出取值相应的概率,属于中档题.
(Ⅱ)①利用独立重复试验的概率公式,可求完成两组练习后,恰好共耗用4发子弹的概率;
②确定ξ可能取值,求出相应的概率,从而可得分布列与期望.
解答:解:(I)设射击5次,恰有2次击中目标的事件为A.
∴
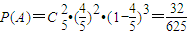 …(4分)
…(4分)(Ⅱ)①完成两组练习后,恰好共耗用4发子弹的事件为B,则
P(B)=0.8•(1-0.8)2•0.8+(1-0.8)•0.8(1-0.8)•0.8+(1-0.8)2•0.8•08=0.0768.…(8分)
②ξ可能取值为1,2,3,4,5.…(9分)
P(ξ=1)=0.8; P(ζ=2)=(1-0.8)•0.8=0.16;
P(ζ=3)=(1-0.8)2•0.8=0.032;P(ζ=4)=(1-0.8)3•0.8=0.0064;
P(ζ=5)=(1-0.8)4•0.8=0.0016…(11分)
ζ的分布列为
| ζ | 1 | 2 | 3 | 4 | 5 |
| P | 0.8 | 0.16 | 0.032 | 0.0064 | 0.00128 |
点评:本题考查独立重复试验的概率,考查离散型随机变量的分布列与期望,解题的关键是求出取值相应的概率,属于中档题.

练习册系列答案
相关题目
 ,且各次射击的结果互不影响.
,且各次射击的结果互不影响.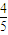 ,且各次射击的结果互不影响.
,且各次射击的结果互不影响.