题目内容
设P是椭圆
+
=1上一点,M、N分别是两圆:(x+4)2+y2=1和(x-4)2+y2=1上的点,则|PM|+|PN|的最小值、最大值分别为
| x2 |
| 25 |
| y2 |
| 9 |
8,12
8,12
.分析:由椭圆的方程可求得其焦点坐标F1(-4,0),F2(4,0),而两圆:(x+4)2+y2=1和(x-4)2+y2=1的圆心分别为两焦点,由于点P为椭圆
+
=1上任意一点,|PF1|+|PF2|=10,由图可知,|PM|+|PN|的最小值为|PF1|+|PF2|-2;|PM|+|PN|的最大值为|PF1|+|PF2|+2;问题可解决.
| x2 |
| 25 |
| y2 |
| 9 |
解答: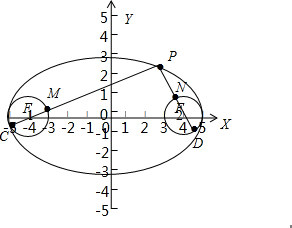 解:∵椭圆方程为
解:∵椭圆方程为
+
=1,∴其焦点坐标为F1(-4,0),F2(4,0),
∴两圆:(x+4)2+y2=1和(x-4)2+y2=1的圆心分别为F1(-4,0),F2(4,0),
又点P为椭圆
+
=1上任意一点,
∴|PF1|+|PF2|=10,
由图可知,|PM|+|PN|的最小值为|PF1|+|PF2|-2=8;
|PM|+|PN|的最大值为|PC|+|PD|=|PF1|+|PF2|+2=12;
故答案为:8,12.
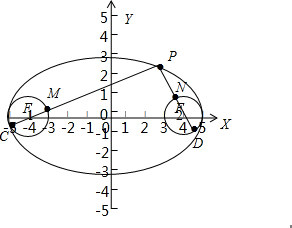 解:∵椭圆方程为
解:∵椭圆方程为| x2 |
| 25 |
| y2 |
| 9 |
∴两圆:(x+4)2+y2=1和(x-4)2+y2=1的圆心分别为F1(-4,0),F2(4,0),
又点P为椭圆
| x2 |
| 25 |
| y2 |
| 9 |
∴|PF1|+|PF2|=10,
由图可知,|PM|+|PN|的最小值为|PF1|+|PF2|-2=8;
|PM|+|PN|的最大值为|PC|+|PD|=|PF1|+|PF2|+2=12;
故答案为:8,12.
点评:本题考查圆与圆锥曲线的综合,关键在于灵活运用椭圆的定义,着重考查数形结合的思想与分析转化的数学思想,考查学生综合分析与解决问题的能力,属于难题.

练习册系列答案
相关题目
设p是椭圆
+
=1上的点.若F1,F2是椭圆的两个焦点,则|PF1|+|PF2|等于( )
| x2 |
| 25 |
| y2 |
| 16 |
| A、4 | B、5 | C、8 | D、10 |