题目内容
盒子中有大小相同的球6个,其中标号为1的球2个,标号为2的球3个.标号为3的球1个,第一次从盒子中任取1个球,放回后第二次再任取1个球 (假设取到每个球的可能性都相同).记第一次与第二次取到球的标号之和为ξ.
(1)求随机变量ξ的分布列:
(2)求随机变量ξ的期望Eξ.
(1)求随机变量ξ的分布列:
(2)求随机变量ξ的期望Eξ.
分析:(1)首先分析题目已知第一次从盒子中任取1个球,放回后第二次再任取1个球.记第一次与第二次取到球的标号之和为ξ.则可分析得到随机变量ξ可以取值是2、3、4、5、6.然后分别求出概率即可得到分布.
(2)由(1)的分布列,再根据期望公式求出期望值即可.
(2)由(1)的分布列,再根据期望公式求出期望值即可.
解答:解:(1)由题意可得,随机变量ξ的取值是2、3、4、5、6.
则随机变量ξ的分布列如下:
P(ξ=2)=
=
P(ξ=3)=
=
P(ξ=4)=
=
,
P(ξ=5)=
=
,
P(ξ=6)=
=
,
∴变量ξ的分布列是:
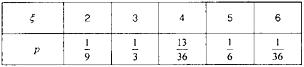
(2)随机变量ξ的期望
Eξ=2×
+3×
+4×
+5×
+6×
=
.
则随机变量ξ的分布列如下:
P(ξ=2)=
| ||||
|
| 1 |
| 9 |
P(ξ=3)=
| ||||
|
| 1 |
| 3 |
P(ξ=4)=
| ||||||||
|
| 13 |
| 36 |
P(ξ=5)=
| ||||
|
| 1 |
| 6 |
P(ξ=6)=
| ||||
|
| 1 |
| 36 |
∴变量ξ的分布列是:

(2)随机变量ξ的期望
Eξ=2×
| 1 |
| 9 |
| 1 |
| 3 |
| 13 |
| 36 |
| 1 |
| 6 |
| 1 |
| 36 |
| 11 |
| 3 |
点评:此题主要考查离散型随机变量的期望的计算问题,对于此类实际应用的问题,需要仔细分析题目中的已知关系,然后对照所学的相关排列组合知识求解即可.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目