Question

用一个过正四棱柱底面一边的平面去截正四棱柱所得的截面是

1. A.
   正方形
2. B.
   矩形
3. C.
   菱形
4. D.
   一般的平行四边形

Answer 1

B
分析：作出满足条件的几何图形，结合正四棱柱的几何特征及面面平行的性质定理，可判断出截面为平行四边形，再由正四棱柱的几何特征及面面垂直的判定及性质定理，可判断出截面为矩形，进而得到结论．
解答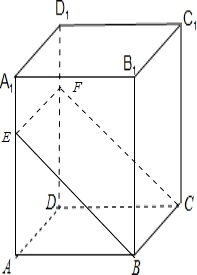：解：如图所示
平面BF为过正四棱柱AC₁底面一边BC的平面
由正四棱柱的几何特征及面面平行的性质定理可得四边形BCFE为平行四边形
又由BC⊥平面AB₁，BE?平面AB₁，
∴BC⊥BE
故四边形BCFE为矩形
故选B
点评：本题以四边形的面积判断为载体考查了空间线面关系的判定及性质，熟练掌握棱柱的结构特征是解答本题的关键．