题目内容
已知a,b,c是不全相等的正数,求证: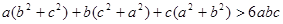
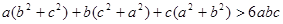
证明:∵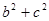 ≥2bc,a>0,
≥2bc,a>0,
∴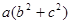 ≥2abc ①…………5分
≥2abc ①…………5分
同理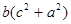 ≥2abc ②
≥2abc ②
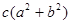 ≥2abc ③…………9分
≥2abc ③…………9分
因为a,b,c不全相等,所以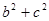 ≥2bc,
≥2bc, 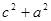 ≥2ca,
≥2ca, 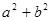 ≥2ab三式不能全取“=”号,从而①、②、③三式也不能全取“=”号
≥2ab三式不能全取“=”号,从而①、②、③三式也不能全取“=”号
∴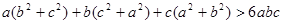 …………14分
…………14分
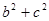 ≥2bc,a>0,
≥2bc,a>0,∴
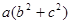 ≥2abc ①…………5分
≥2abc ①…………5分同理
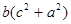 ≥2abc ②
≥2abc ②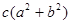 ≥2abc ③…………9分
≥2abc ③…………9分因为a,b,c不全相等,所以
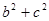 ≥2bc,
≥2bc, 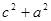 ≥2ca,
≥2ca, 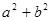 ≥2ab三式不能全取“=”号,从而①、②、③三式也不能全取“=”号
≥2ab三式不能全取“=”号,从而①、②、③三式也不能全取“=”号∴
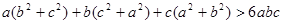 …………14分
…………14分可以采用分析法进行推证,然后采用综合法书写解题步骤.
因为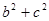 ≥2bc,
≥2bc, 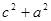 ≥2ca,
≥2ca, 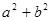 ≥2ab,然后根据同向正向不等式具有可乘性,同向不等式具有可加性,还要注意取等的条件,问题易解.
≥2ab,然后根据同向正向不等式具有可乘性,同向不等式具有可加性,还要注意取等的条件,问题易解.
因为
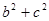 ≥2bc,
≥2bc, 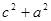 ≥2ca,
≥2ca, 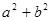 ≥2ab,然后根据同向正向不等式具有可乘性,同向不等式具有可加性,还要注意取等的条件,问题易解.
≥2ab,然后根据同向正向不等式具有可乘性,同向不等式具有可加性,还要注意取等的条件,问题易解.
练习册系列答案
相关题目
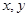 ,满足
,满足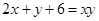 ,则
,则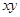 的最小值是 __ .
的最小值是 __ .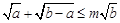 恒成立,则m的最小值是 。
恒成立,则m的最小值是 。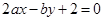
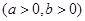 被圆
被圆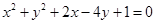 截得的弦长为4,则
截得的弦长为4,则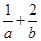 的最小值为___________.
的最小值为___________.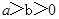 ,则
,则 的最小值是 ( )
的最小值是 ( )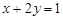 ,则
,则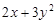 的最小值是 ▲ .
的最小值是 ▲ .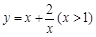 的值域为( )
的值域为( )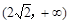
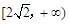
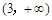
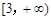
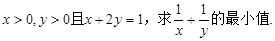 .
.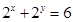 ,则
,则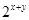 的最大值是
的最大值是