题目内容
(5分)(2011•重庆)若△ABC的内角A,B,C满足6sinA=4sinB=3sinC,则cosB=( )
A.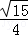 | B.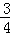 | C.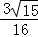 | D.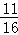 |
D
解析试题分析:由题意利用正弦定理,推出a,b,c的关系,然后利用余弦定理求出cosB的值.
解:△ABC的内角A,B,C满足6sinA=4sinB=3sinC,所以6a=4b=3c,不妨令a=2,b=3,c=4,
所以由余弦定理:b2=a2+c2﹣2accosB,所以cosB=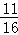 ,
,
故选D.
点评:本题是基础题,考查正弦定理,余弦定理的应用,考查计算能力,常考题型.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
△ABC中,若sinA<cosB,则△ABC为
| A.锐角三角形 | B.直角三角形 | C.钝角三角形 | D.不能确定 |
在△ABC中,角A,B,C所对的边分别是a,b,c,若 ,则△ABC的形状是( )
,则△ABC的形状是( )
| A.等腰三角形 | B.直角三角形 | C.等腰直角三角形 | D.等腰或直角三角形 |
在 中,由已知条件解三角形,其中有两解的是( )
中,由已知条件解三角形,其中有两解的是( )
A.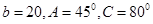 | B. |
C. | D. |
在 中,若
中,若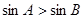 ,则
,则 与
与 的大小关系为( )
的大小关系为( )
A.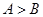 | B.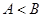 | C. | D. 、 、 的大小关系不能确定 的大小关系不能确定 |
[2014·浙江绍兴一模]在湖面上高为10 m处测得天空中一朵云的仰角为30°,测得湖中之影的俯角为45°,则云距湖面的高度为(精确到0.1 m)( )
| A.2.7 m | B.17.3 m | C.37.3 m | D.373 m |
在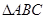 中,角A,B,C的对边分别为
中,角A,B,C的对边分别为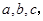 若
若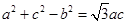 ,则角B的值为( )
,则角B的值为( )
A.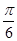 | B. | C. | D.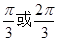 |
 中,角
中,角 的对边分别为
的对边分别为 ,若点
,若点 在直线
在直线 上,则角
上,则角 的值为( )
的值为( ) B.
B.