题目内容
函数y＝lg(3－4x＋x2)的定义域为M，当x∈M时，求 f(x)＝2x＋2－3×4x的最值．
解：由3－4x＋x2>0，得x>3或x<1，
∴M＝{x|x>3或x<1}，
f(x)＝－3×(2x)2＋2x＋2＝－3(2x－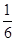
)2＋
.
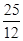∵x>3或x<1，∴2x>8或0<2x<2，
∴当2x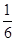＝，即x＝log2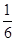时， f(x)最大，最大值为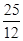， f(x)没有最小值．
∴M＝{x|x>3或x<1}，
f(x)＝－3×(2x)2＋2x＋2＝－3(2x－
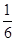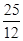)2＋.∵x>3或x<1，∴2x>8或0<2x<2，
∴当2x＝
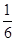，即x＝log2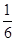时， f(x)最大，最大值为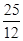， f(x)没有最小值．略
练习册系列答案
相关题目
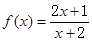，试证明f(x)在区间(-2,+∞)上是增函数，并求出该函数在区间[1,4]上的最大值和最小值.
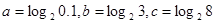,则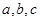
的大小关系为( )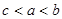
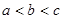
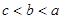
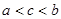
是定义域为R的奇函数．
时，试判断函数单调性并求不等式f(x2＋2x)＋f(x－4)>0的解集；
恒成立的
的取值范围；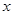
年后，我国人口数大约为（ ）
；
；
；
.
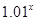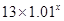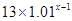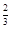＋lg4＋2lg5＝__________
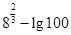的值为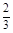 
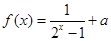是奇函数，则
．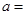