题目内容
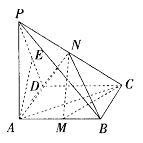
PA⊥矩形ABCD平面，M，N分别是AB、PC的中点．①求证：MN⊥AB；
②若PA︰PD＝1︰
，求证：MN⊥PC；
③在②成立的条件下，设PA＝a，求异面直线AB与PC的距离．
答案：
解析：
解析：
解：①连接AC、PB、BN、AN．由PA⊥平面ABCD，知PA⊥AC，Rt△ACD中，PN=CN， ．因为BC⊥AB，AB是PB在平面ABCD的射影，所以BC⊥PB．Rt△PBC中，PN=CN， ，故AN=BN，等腰△ABN中，M是AB中点，故MN⊥AB．如图．
②设PD中点为E，AB⊥AE，由CD//AB，知CD⊥AE，Rt△PAD中，因为PA︰PD=1︰ ③MN是异面直线AB、PC的公垂线段，MN=AE，PA=a，Rt△PAD中，PA︰AD=1︰
|
，所以PA=AD，又E是PD中点，AE⊥PD，AE⊥平面PDC，故AE⊥PC，MN//AE，因此MN⊥PC．
，故
．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
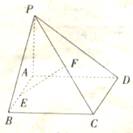（13分）如图3，已知矩形ABCD所在平面外一点P，PA⊥平面ABCD，E、F分别是AB，PC的中点。
（13分）如图3，已知矩形ABCD所在平面外一点P，PA⊥平面ABCD，E、F分别是AB，PC的中点。