题目内容
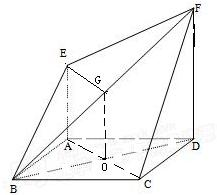 如右图,已知ABCD为正方形,AE⊥平面ABCD,DF⊥平面ABCD,AD=DF=2AE=2.
如右图,已知ABCD为正方形,AE⊥平面ABCD,DF⊥平面ABCD,AD=DF=2AE=2.(1)求证:平面BEF⊥平面BDF;
(2)求点A到平面BEF的距离;
(3)求平面BEF与平面BCD所成的二面角的大小.
分析:对于(1),要证明平面BEF⊥平面BDF,只需在平面平面BEF内找一条直线垂直于平面平BDF即可,
而AE⊥平面ABCD,DF⊥平面ABCD,故连接AC交BD于O,取BF的中点G,连EG,只证EG垂直于平面BDF,
而AO垂直于平面BDF,只证EG∥AO即可;
对于(2),由EG∥AO,AO∥平面BEF,O到平面BEF的距离就是A到平面BEF的距离,由面面垂直的性质定理,
只需过O向BF作垂线,利用相似三角形求出此垂线段的长度即可;
对于(3),由(1)、(2)知:平面ABD为平面BEF的射影,由射影定理容易求二面角的余弦值,从而可求.
而AE⊥平面ABCD,DF⊥平面ABCD,故连接AC交BD于O,取BF的中点G,连EG,只证EG垂直于平面BDF,
而AO垂直于平面BDF,只证EG∥AO即可;
对于(2),由EG∥AO,AO∥平面BEF,O到平面BEF的距离就是A到平面BEF的距离,由面面垂直的性质定理,
只需过O向BF作垂线,利用相似三角形求出此垂线段的长度即可;
对于(3),由(1)、(2)知:平面ABD为平面BEF的射影,由射影定理容易求二面角的余弦值,从而可求.
解答:解:(1)连AC交BD于O,取BF的中点G,连EG
∵OG
DF,AE
DF∴OG
AE
∴四边形AOGE是平行四边形∴AO
EG
∵DF⊥平面ABCD
∴DF⊥AO又AO⊥BD
∴AO⊥平面BDF
∴EG⊥平面BDF
∵EG?平面BEF
∴平面BEF⊥平面BDF
(2)由(1)知AO∥EG
∴AO∥平面BEF
∴O到平面BEF的距离就是A到平面BEF的距离
过O作OH⊥BF于H
∵平面BEF⊥平面BDF∴OH⊥平面BEF
∵△BOH\~△BFD∴
=
∴OH=
即点A到平面BEF的距离为
.
(3)设平面BEF与平面BCD所成的角为θ
∵cosθ=
=
∴平面BEF与平面BCD所成的二面角的大小为:arccos
∵OG
| ||
. |
| 1 |
| 2 |
| ||
. |
| 1 |
| 2 |
| ||
. |
∴四边形AOGE是平行四边形∴AO
| ||
. |
∵DF⊥平面ABCD
∴DF⊥AO又AO⊥BD
∴AO⊥平面BDF
∴EG⊥平面BDF
∵EG?平面BEF
∴平面BEF⊥平面BDF
(2)由(1)知AO∥EG
∴AO∥平面BEF
∴O到平面BEF的距离就是A到平面BEF的距离
过O作OH⊥BF于H
∵平面BEF⊥平面BDF∴OH⊥平面BEF
∵△BOH\~△BFD∴
| OH |
| DF |
| OB |
| BF |
| ||
| 3 |
即点A到平面BEF的距离为
| ||
| 3 |
(3)设平面BEF与平面BCD所成的角为θ
∵cosθ=
| S△ABD |
| S△BEF |
| ||
| 3 |
∴平面BEF与平面BCD所成的二面角的大小为:arccos
| ||
| 3 |
点评:本题考查面面垂直的判定,点到面的距离,以及二面角的求法,要注意将面面垂直转化为线面垂直,点到平面距离问题中的点的转化,二面角平面角求法中的射影定理的应用.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目

 ,
, ,
, .
. 平面
平面 ;
;
 如右图,已知ABCD为正方形,AE⊥平面ABCD,DF⊥平面ABCD,AD=DF=2AE=2.
如右图,已知ABCD为正方形,AE⊥平面ABCD,DF⊥平面ABCD,AD=DF=2AE=2.