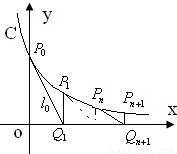
题目内容
过P(1,0)做曲线C:xy=1,x∈(0,+∞),的切线,切点为Q1,设Q1在x轴上的投影为P1,又过P1做曲线C的切线,切点为Q2,设Q2在x轴上的投影为P2,…,依次下去得到一系列点Q1、Q2、Q3、…、Qn的横坐标为an.(1)求a1的值.
(2)求证数列{an}是等比数列.
(3)设
 ,问是否存在实数m,使得对于任意的正整数M,N,都有|bM-bN|<m恒成立.若存在,求出m;不存在,说明理由.
,问是否存在实数m,使得对于任意的正整数M,N,都有|bM-bN|<m恒成立.若存在,求出m;不存在,说明理由.
【答案】分析:(1)由题意可设切点Qn(an,ank),根据导数的几何意义可求切线方程,当n=1时由切线过点P(1,0)可求a1
(2)由切线过点Pn-1(an-1,0),代入整理可得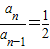 ,可证
,可证
(3)由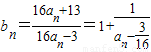 ,构造函数
,构造函数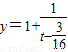 ,
,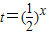 ,由复合函数单调性可求数列{bn}的最大项与最小项,而|bM-bN|<|bn(最大值)-bn(最小值)|,可求m
,由复合函数单调性可求数列{bn}的最大项与最小项,而|bM-bN|<|bn(最大值)-bn(最小值)|,可求m
解答:解:(1)y'=-x-2,若切点是Qn(an,ank),
则切线方程为y-an-1=-an-2(x-an).
当n=1时,切线过点P(1,0)
即0-a1-1=-a1-2(1-a1).得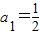 .
.
(2)当n>1时,切线过点Pn-1(an-1,0)
即0-an-1=-an-2(an-1-an).得 .
.
∴数列{an}是首项为 ,公比为
,公比为 的等比数列.
的等比数列.
∴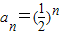 .…(6分)
.…(6分)
(3)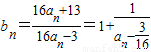
令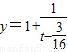 ,
,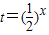 (8分)
(8分)
由复合函数单调性可知
当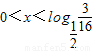 时,y<0.且单调递增.
时,y<0.且单调递增.
当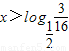 时,y>0.且单调递增.
时,y>0.且单调递增.
所以当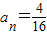 ,即n=2,时,b2=17为最大值
,即n=2,时,b2=17为最大值
当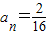 ,即n=3,时,b3=-15为最小值 (13分)
,即n=3,时,b3=-15为最小值 (13分)
|bM-bN|<|b3-b2|=32
所以m>32 …(15分)
点评:本题主要考查了利用函数的导数求解曲线在某点的切线方程,等比数列通项公式的求解及利用复合函数单调性判断数列的单调性进而求解数列的最大项及最小项,属于函数与数列知识的综合应用.
(2)由切线过点Pn-1(an-1,0),代入整理可得
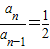 ,可证
,可证(3)由
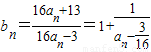 ,构造函数
,构造函数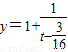 ,
,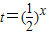 ,由复合函数单调性可求数列{bn}的最大项与最小项,而|bM-bN|<|bn(最大值)-bn(最小值)|,可求m
,由复合函数单调性可求数列{bn}的最大项与最小项,而|bM-bN|<|bn(最大值)-bn(最小值)|,可求m解答:解:(1)y'=-x-2,若切点是Qn(an,ank),
则切线方程为y-an-1=-an-2(x-an).
当n=1时,切线过点P(1,0)
即0-a1-1=-a1-2(1-a1).得
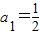 .
.(2)当n>1时,切线过点Pn-1(an-1,0)
即0-an-1=-an-2(an-1-an).得
 .
.∴数列{an}是首项为
 ,公比为
,公比为 的等比数列.
的等比数列.∴
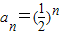 .…(6分)
.…(6分)(3)
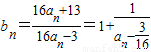
令
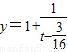 ,
,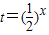 (8分)
(8分)由复合函数单调性可知
当
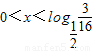 时,y<0.且单调递增.
时,y<0.且单调递增.当
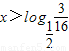 时,y>0.且单调递增.
时,y>0.且单调递增.所以当
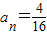 ,即n=2,时,b2=17为最大值
,即n=2,时,b2=17为最大值当
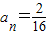 ,即n=3,时,b3=-15为最小值 (13分)
,即n=3,时,b3=-15为最小值 (13分)|bM-bN|<|b3-b2|=32
所以m>32 …(15分)
点评:本题主要考查了利用函数的导数求解曲线在某点的切线方程,等比数列通项公式的求解及利用复合函数单调性判断数列的单调性进而求解数列的最大项及最小项,属于函数与数列知识的综合应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
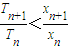 (n∈N+).
(n∈N+).