题目内容
函数y=cos(2x+
)的图象（ ）
| π |
| 3 |
A、关于点（
| ||
B、关于点（
| ||
C、关于直线x=
| ||
D、关于直线x=
|
考点：余弦函数的图象
专题：三角函数的图像与性质
分析：分别根据余弦函数的图象判断函数的对称中心和对称轴即可．
解答：解：∵函数y=cos(2x+
)，
∴当x=
时，y=cos(2×
+
)=cosπ=-1为最小值，∴函数关于直线x=
对称，
当x=
时，y=cos?(2×
+
)=cos?
≠0，也不是最值，
∴A，B，C错误，
故选：D．
| π |
| 3 |
∴当x=
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
当x=
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| 2π |
| 3 |
∴A，B，C错误，
故选：D．
点评：本题主要考查余弦函数的图象和性质，要求熟练掌握三角函数对称轴和对称中心的判断方法．
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
名师点睛字词句段篇系列答案
相关题目
已知a为执行如图所示的程序框图输出的结果，则二项式（a| x |
| 1 | ||
|
| A、192 | B、32 |
| C、96 | D、-192 |
我国古代“五行”学说认为：“物质分金、木、土、水、火五种属性，金克木，木克土，土克水，水克火，火克金．”将这五种不同属性的物质任意排成一列，设事件A表示“排列中属性相克的两种物质均不相邻”，则事件A发生的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，点A，B是单位圆O上的两点，点C是圆O与x轴正半轴的交点，将锐角α的终边OA按逆时针方向旋转函数y=
在区间[-π，π]上的图象是（ ）
| xcosx |
| x2+1 |
A、 |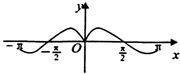
B、 |
C、 |
D、 |
已知向量
=（2，4），
=（-1，1），则2
-
=（ ）
| a |
| b |
| a |
| b |
| A、（5，7） |
| B、（5，9） |
| C、（3，7） |
| D、（3，9） |
如图，在四面体OABC中，AC=BC，|
|=3，|
|=1，则
•
=（ ）
| OA |
| OB |
| OC |
| BA |
| A、8 | B、6 | C、4 | D、3 |
在△ABC中，A=
，AB=3
，AC=3，D在边BC上，且CD=2DB，则AD=（ ）
| π |
| 6 |
| 3 |
A、
| ||
B、
| ||
| C、5 | ||
D、2
|
已知命题p，q，则“p∧（?q）为真”是“（?p）∨q为假”的（ ）
| A、充分不必要条件 | B、必要不充分条件 | C、充要条件 | D、既不充分也不必要条件 |