题目内容
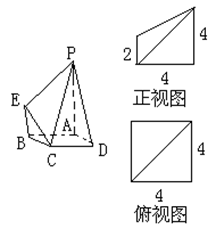
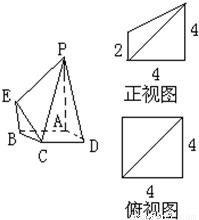
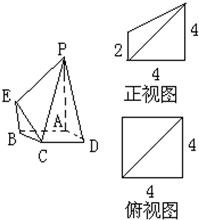 右图是一几何体的直观图、正视图和俯视图.
右图是一几何体的直观图、正视图和俯视图.(I)在正视图右侧,按照画三视图的要求画出该几何体的侧视图;
(II)在所给直观图中连接BD,证明BD∥面PEC;
(III)按照给出的尺寸,求该几何体的体积.
分析:(I)在正视图右侧,直接按照画三视图的要求画出该几何体的侧视图;
(II)在所给直观图中连接BD,要证BD∥面PEC,只需取PC的中点M,设AC与BD的交点为N,连接MN、ME,证明EM∥BN,就是EM∥BD,然后说明BD∥面PEC;
(III)按照给出的尺寸,几何体的体积转化为两个棱锥VC-ABEP,VP-ACD的体积的和.
(II)在所给直观图中连接BD,要证BD∥面PEC,只需取PC的中点M,设AC与BD的交点为N,连接MN、ME,证明EM∥BN,就是EM∥BD,然后说明BD∥面PEC;
(III)按照给出的尺寸,几何体的体积转化为两个棱锥VC-ABEP,VP-ACD的体积的和.
解答: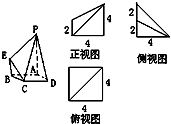 解(I)如图所示.
解(I)如图所示.
(II)证明,取PC的中点M,设AC与BD的交点为N,连接MN、ME,∵PM=CM,AN=CN∴MN=
PA,MN∥PA
∴MN=EB,MN∥EB,故BEMN为平行四边形.
∴EM∥BN,又EM?平面PEC,BD?面PEC,∴BD∥平面PEC.
(III)V=VC-ABEP+VP-ACD=
×
×(2+4)×4×4+
×
×4×4×4=
 解(I)如图所示.
解(I)如图所示.(II)证明,取PC的中点M,设AC与BD的交点为N,连接MN、ME,∵PM=CM,AN=CN∴MN=
| 1 |
| 2 |
∴MN=EB,MN∥EB,故BEMN为平行四边形.
∴EM∥BN,又EM?平面PEC,BD?面PEC,∴BD∥平面PEC.
(III)V=VC-ABEP+VP-ACD=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 80 |
| 3 |
点评:本题是中档题,考查几何体的三视图的画法,直线与平面平行的证明方法,几何体的体积的求法,考查空间想象能力,计算能力,逻辑推理能力;注意三视图的画图的要求等等.

练习册系列答案
相关题目
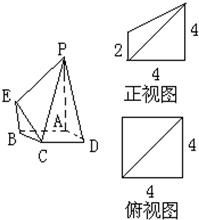 右图是一几何体的直观图、正视图和俯视图.
右图是一几何体的直观图、正视图和俯视图.