题目内容
已知集合A={x|x2+a≤(a+1)x, a∈R},若存在a∈R,使得集合A中所有整数元素之和为28,则实数a的取值范围是( )
| A.[9,10) | B.[7,8) | C.(9,10) | D.[7,8] |
B
注意到不等式x2+a≤(a+1)x,即(x-a)(x-1)≤0,
因此该不等式的解集中必有1与a.
要使集合A中所有整数元素之和为28,必有a>1.
注意到以1为首项、1为公差的等差数列的前7项和为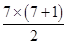 =28,
=28,
因此由集合A中所有整数元素之和为28得7≤a<8,
即实数a的取值范围是[7,8).
因此该不等式的解集中必有1与a.
要使集合A中所有整数元素之和为28,必有a>1.
注意到以1为首项、1为公差的等差数列的前7项和为
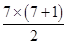 =28,
=28,因此由集合A中所有整数元素之和为28得7≤a<8,
即实数a的取值范围是[7,8).

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
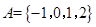 ,
,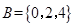 ,则
,则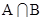 = .
= .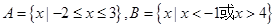 ,则集合
,则集合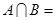 ( )
( )
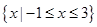
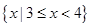
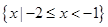
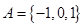 ,
,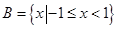 ,则
,则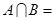 ( )
( )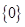
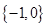
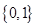
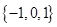
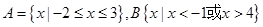 ,则集合
,则集合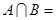 ( )
( )
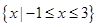
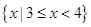
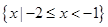
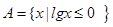 ,B=
,B=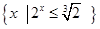 ,则A∪B=( )
,则A∪B=( )