题目内容
已知等差数列 的首项
的首项 及公差
及公差 都是整数,前
都是整数,前 项和为
项和为 ,若
,若 ,设
,设 的结果为 。
的结果为 。
【答案】
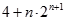
【解析】解:因为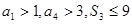
所以a1+3d>3,3a2≤9⇒d>2/ 3 ,a1+d≤3⇒a1≤3-d<3-2 /3 =7 /3.
∵等差数列{an}的首项a1及公差d都是整数
∴a1=2 则1/ 3 <d≤1⇒d=1.
∴an=2+1×(n-1)=n+1.
∴bn=2nan=2n(n+1)
令Sn=b1+b2+…+bn
=2•21+3•22+…+n•2n-1+(n+1)•2n①
∴2Sn=2•22+3•23+…+n•2n+(n+1)2n+1②
①-②得,-Sn=2•21+22+…+2n-(n+1)•2n+1=-n•2n+1-4
∴Sn=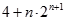
故答案为: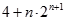

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目

 的首项
的首项 及公差
及公差 都是整数,前
都是整数,前 项和为
项和为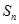 ,若
,若 ,设
,设 的结果为 。
的结果为 。 的首项
的首项 及公差
及公差 都是整数,前
都是整数,前 项和为
项和为 ,若
,若 ,设
,设 的结果为 .
的结果为 . 的首项
的首项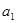 及公差
及公差 都是整数,且前
都是整数,且前 项和为
项和为 ,若
,若 ,则数列
,则数列 的首项
的首项 及公差
及公差 都是整数,且前
都是整数,且前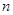 项和为
项和为 ,若
,若 ,则数列
,则数列