题目内容
为考察某种甲型H1N1疫苗的效果，进行动物实验，得到如下疫苗效果的实验列联表：
设从没服用疫苗的动物中任取1只，感染数为ξ；
（1）若P(ξ=0)=
，请将上面的2×2列联表补充完整；
（2）能够以95%的把握认为这种甲型H1N1疫苗有效吗？并说明理由．
| 感染 | 未感染 | 合计 | |
| 没服用 | 30 | ||
| 服用 | 10 | ||
| 合计 | 100 |
（1）若P(ξ=0)=
| 3 |
| 5 |
（2）能够以95%的把握认为这种甲型H1N1疫苗有效吗？并说明理由．
分析：（1）没服用疫苗的动物共有m只，根据所给的变量ξ=0概率，得到关于m的方程，解方程即可，做出要求的值，即可列出2×2列联表．
（2）根据所给的数据做出观测值，把观测值同临界值进行比较得到能够以95%的把握认为这种甲型H1N1疫苗有效．
（2）根据所给的数据做出观测值，把观测值同临界值进行比较得到能够以95%的把握认为这种甲型H1N1疫苗有效．
解答：解：（1）没服用疫苗的动物共有m只，∵P(ξ=0)=
，∴
=
，∴m=50…（3分）
则得到2×2列联表如下：
…（6分）
（2）设不被感染与服用甲型H1N1疫苗无关，由上述2×2列联表可得
所以能够以95%的把握认为这种甲型H1N1疫苗有效 …（12分）
| 3 |
| 5 |
| 30 |
| m |
| 3 |
| 5 |
则得到2×2列联表如下：
| 感染 | 未感染 | 合计 | |
| 没服用 | 20 | 30 | 50 |
| 服用 | 10 | 40 | 50 |
| 合计 | 30 | 70 | 100 |
（2）设不被感染与服用甲型H1N1疫苗无关，由上述2×2列联表可得
|
所以能够以95%的把握认为这种甲型H1N1疫苗有效 …（12分）
点评：本题考查独立性检验的应用，本题解题的关键是正确运算出要用的观测值，把观测值同临界值进行比较，理解概率的意义．
练习册系列答案
相关题目
为考察某种甲型H1N1疫苗的效果，进行动物实验，得到如下疫苗效果的实验列联表：
设从没服用疫苗的动物中任取两只，感染数为ξ，从服从过疫苗的动物中任取两只，感染数为η，工作人员曾计算过P（ξ=2）=
P（η=2）
（1）求出列联表中数据x，y，M，N的值；
（2）写出ξ与η的均值（不要求计算过程），并比较大小，请解释所得出的结论的实际意义；
（3）能够以97.5%的把握认为这种甲型H1N1疫苗有效么？并说明理由．
参考数据：
| 感染 | 未感染 | 总计 | |
| 没服用 | 20 | 30 | 50 |
| 服用 | x | y | 50 |
| 总计 | M | N | 100 |
| 38 |
| 9 |
（1）求出列联表中数据x，y，M，N的值；
（2）写出ξ与η的均值（不要求计算过程），并比较大小，请解释所得出的结论的实际意义；
（3）能够以97.5%的把握认为这种甲型H1N1疫苗有效么？并说明理由．
参考数据：
| P（K2≥k0） | 0.05 | 0.025 | 0.010 |
| k0 | 3.841 | 5.024 | 6.635 |
（本题满分12分）
为考察某种甲型H1N1疫苗的效果，进行动物实验，得到如下疫苗效果的实验列联表：
|
|
感染 |
未感染 |
总计 |
|
没服用 |
20 |
30 |
50 |
|
服用 |
x |
y |
50 |
|
总计 |
M |
N |
100 |
设从没服用疫苗的动物中任取两只，感染数为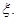
从服从过疫苗的动物中任取两只，感染数为
工作人员曾计算过
（1）求出列联表中数据
的值；
（2）写出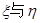
的均值（不要求计算过程），并比较大小，请解释所得出的结论的实际意义；
（3）能够以97.5%的把握认为这种甲型H1N1疫苗有效么？并说明理由。
参考公式：
参考数据：
|
|
0．05 |
0．025 |
0．010 |
|
|
3．841 |
5．024 |
6．635 |
