题目内容
下列命题中所有假命题的序号为 .①y=sinxcosx的周期为π,最大值为
 ; ②若x是第一象限的角,则y=sinx是增函数;③在△ABC中,若sinA=sinB,则A=B; ④f(x)=sinx+cosx既不是奇函数,也不是偶函数; ⑤
; ②若x是第一象限的角,则y=sinx是增函数;③在△ABC中,若sinA=sinB,则A=B; ④f(x)=sinx+cosx既不是奇函数,也不是偶函数; ⑤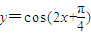 的一条对称轴为
的一条对称轴为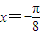 .
.
【答案】分析:①把函数解析式利用二倍角的正弦函数公式化简为一个角的正弦函数,找出ω的值,代入周期公式T= ,即可求出函数的最小正周期,同时根据正弦函数的值域即可得到函数的最大值,进而做出判断;
,即可求出函数的最小正周期,同时根据正弦函数的值域即可得到函数的最大值,进而做出判断;
②可举一个反例,比如390°>30°,且两角都为第一象限角,但是两角的正弦值相等,故此函数在第一象限不是增函数,本选项为假命题;
③在△ABC中,若sinA=sinB,得到两角相等或互补,但是两角为三角形的内角,可得两角不可能互补,故两角相等,本选项为真命题;
④把函数解析式利用特殊角的正弦函数及两角和与差的正弦函数公式化为一个角的正弦函数,根据正弦函数为奇函数可得原函数也为奇函数,故本选项为假命题;
⑤根据余弦函数的对称性,令角度为kπ,求出x的值即为函数的对称轴,即可作出判断.
解答:解:①y=sinxcosx= sin2x,
sin2x,
∵ω=2,∴T= =π,
=π,
又sin2x∈[-1,1],
∴函数的最大值为 ,本选项为真命题;
,本选项为真命题;
②由于390°>30°,且都是第一象限角,sin390°=sin30°= ,
,
故函数y=sinx在第一象限不是增函数,本选项为假命题;
③在△ABC中,若sinA=sinB,得到A=B或A+B=π(舍去),
∴A=B,本选项为真命题;
④f(x)=sinx+cosx= sin(x+
sin(x+ ),
),
∵正弦函数sin(x+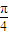 )为奇函数,
)为奇函数,
∴函数f(x)=sinx+cosx为奇函数,本选项为假命题;
⑤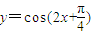 ,
,
令2x+ =kπ,解得x=
=kπ,解得x= -
- ,
,
当k=0时,函数的对称轴为x=- ,
,
∴函数的一条对称轴为 ,本选项为真命题,
,本选项为真命题,
故答案为:②④
点评:此题考查了二倍角的正弦函数公式,两角和与差的正弦函数公式,正弦函数的定义域与值域,正弦函数的奇偶性,以及余弦函数的对称性,熟练掌握正弦、余弦函数的图象与性质是解本题的关键.
 ,即可求出函数的最小正周期,同时根据正弦函数的值域即可得到函数的最大值,进而做出判断;
,即可求出函数的最小正周期,同时根据正弦函数的值域即可得到函数的最大值,进而做出判断;②可举一个反例,比如390°>30°,且两角都为第一象限角,但是两角的正弦值相等,故此函数在第一象限不是增函数,本选项为假命题;
③在△ABC中,若sinA=sinB,得到两角相等或互补,但是两角为三角形的内角,可得两角不可能互补,故两角相等,本选项为真命题;
④把函数解析式利用特殊角的正弦函数及两角和与差的正弦函数公式化为一个角的正弦函数,根据正弦函数为奇函数可得原函数也为奇函数,故本选项为假命题;
⑤根据余弦函数的对称性,令角度为kπ,求出x的值即为函数的对称轴,即可作出判断.
解答:解:①y=sinxcosx=
 sin2x,
sin2x,∵ω=2,∴T=
 =π,
=π,又sin2x∈[-1,1],
∴函数的最大值为
 ,本选项为真命题;
,本选项为真命题;②由于390°>30°,且都是第一象限角,sin390°=sin30°=
 ,
,故函数y=sinx在第一象限不是增函数,本选项为假命题;
③在△ABC中,若sinA=sinB,得到A=B或A+B=π(舍去),
∴A=B,本选项为真命题;
④f(x)=sinx+cosx=
 sin(x+
sin(x+ ),
),∵正弦函数sin(x+
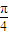 )为奇函数,
)为奇函数,∴函数f(x)=sinx+cosx为奇函数,本选项为假命题;
⑤
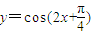 ,
,令2x+
 =kπ,解得x=
=kπ,解得x= -
- ,
,当k=0时,函数的对称轴为x=-
 ,
,∴函数的一条对称轴为
 ,本选项为真命题,
,本选项为真命题,故答案为:②④
点评:此题考查了二倍角的正弦函数公式,两角和与差的正弦函数公式,正弦函数的定义域与值域,正弦函数的奇偶性,以及余弦函数的对称性,熟练掌握正弦、余弦函数的图象与性质是解本题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 的否定是
的否定是 ;
;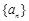 前
前 项和为
项和为 ,则三点
,则三点 共线;
共线; 上单调递减;
上单调递减; 中,若
中,若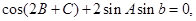 则
则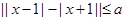 恒成立,则实数
恒成立,则实数 的取值范围是
的取值范围是 。
。