题目内容
已知函数 ,若函数
,若函数 满足
满足 =-
=-
(1)求实数a的值。 (2)判断函数的单调性
 ,若函数
,若函数 满足
满足 =-
=-
(1)求实数a的值。 (2)判断函数的单调性
(1)a=1 (2) 在定义域R上为增函数
在定义域R上为增函数
 在定义域R上为增函数
在定义域R上为增函数本试题主要是考查了函数奇偶性和单调性的运用。
(1)利用奇函数的定义可知,f(-x)=-f(x)对任意的x都成立,得到参数a的值。
(2);利用定义法作差,判定单调性证明。
解:(1)由题,函数的定义域为R. ………2分
∵ =-
=-
∴ =-
=- ,即
,即 =0.
=0.
∴ 。解得,a=1 ………6分
。解得,a=1 ………6分
(2) 任取 ………7分
………7分
则 ,………10分
,………10分
∴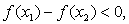 即
即
∴ 在定义域R上为增函数。 ………12分
在定义域R上为增函数。 ………12分
(1)利用奇函数的定义可知,f(-x)=-f(x)对任意的x都成立,得到参数a的值。
(2);利用定义法作差,判定单调性证明。
解:(1)由题,函数的定义域为R. ………2分
∵
 =-
=-
∴
 =-
=- ,即
,即 =0.
=0.∴
 。解得,a=1 ………6分
。解得,a=1 ………6分(2) 任取
 ………7分
………7分则
 ,………10分
,………10分∴
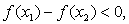 即
即
∴
 在定义域R上为增函数。 ………12分
在定义域R上为增函数。 ………12分
练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
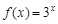 ,且
,且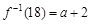 ,且
,且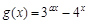 的定义域为[0, 1]
的定义域为[0, 1]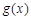 的表达式
的表达式 ,
, 表示不超过实数m的最大整数,则函数
表示不超过实数m的最大整数,则函数 的值域是( )
的值域是( )



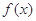 的定义域为
的定义域为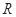 ,对于
,对于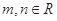 ,恒有
,恒有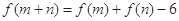 ,且
,且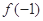 是不大于5 的正整数,当
是不大于5 的正整数,当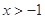 时,
时,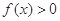 .那么具有这种性质的函数
.那么具有这种性质的函数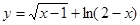 的定义域是( )
的定义域是( )



 的定义域是
的定义域是 ,则
,则 的定义域是( )
的定义域是( )



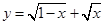 的定义域为( )
的定义域为( )



 的定义域是________
的定义域是________ 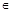 [-1,1]时,函数f(x)=3x-2的值域为
[-1,1]时,函数f(x)=3x-2的值域为