题目内容
(本小题满分13分)若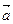 =
=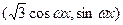 ,
,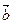 =
=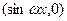 ,其中
,其中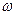 >0,记函数f(x)=(
>0,记函数f(x)=(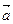 +
+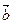 )·
)·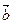 +k.
+k.
(1)若f(x)图象中相邻两条对称轴间的距离不小于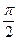 ,求
,求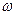 的取值范围.
的取值范围.
(2)若f(x)的最小正周期为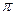 ,且当x
,且当x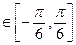 时,f(x)的最大值是
时,f(x)的最大值是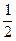 ,求f(x)的解析式,
,求f(x)的解析式,
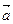 =
=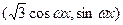 ,
,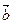 =
=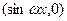 ,其中
,其中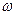 >0,记函数f(x)=(
>0,记函数f(x)=(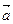 +
+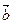 )·
)·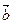 +k.
+k.(1)若f(x)图象中相邻两条对称轴间的距离不小于
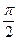 ,求
,求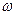 的取值范围.
的取值范围.(2)若f(x)的最小正周期为
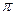 ,且当x
,且当x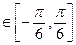 时,f(x)的最大值是
时,f(x)的最大值是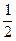 ,求f(x)的解析式,
,求f(x)的解析式,(1)0<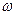 ≤1
≤1
(2)f(x)=sin(2x-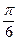 )
)
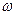 ≤1
≤1(2)f(x)=sin(2x-
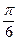 )
)∵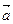 =
=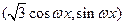
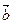 =
=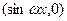 ∴
∴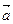 +
+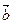 =
=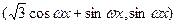
故f(x)=(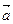 +
+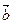 )·
)·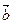 +k=
+k=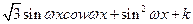
=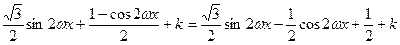
=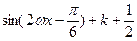 …………………………4分
…………………………4分
(1)由题意可知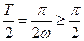 ,∴
,∴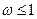 又
又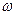 >0,∴0<
>0,∴0<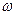 ≤1 …………6分
≤1 …………6分
( 2)∵T=
2)∵T=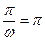 ,∴
,∴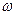 =1 ∴f(x)=sin(2x-
=1 ∴f(x)=sin(2x-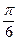 )+k+
)+k+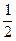
∵x∈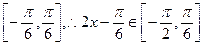 ………………8分
………………8分
从而当2x-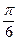 =
=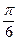 即x
即x =
=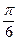 时fmax(x)=f(
时fmax(x)=f(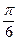 )=sin
)=sin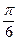 +k+
+k+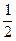 =k+1=
=k+1=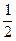
∴k=-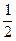 故f(x)=sin(2x-
故f(x)=sin(2x-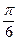 )…………………12分
)…………………12分
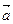 =
=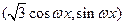
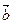 =
=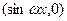 ∴
∴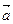 +
+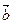 =
=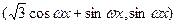
故f(x)=(
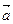 +
+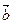 )·
)·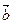 +k=
+k=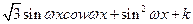
=
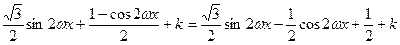
=
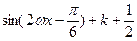 …………………………4分
…………………………4分(1)由题意可知
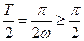 ,∴
,∴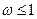 又
又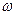 >0,∴0<
>0,∴0<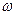 ≤1 …………6分
≤1 …………6分(
 2)∵T=
2)∵T=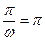 ,∴
,∴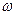 =1 ∴f(x)=sin(2x-
=1 ∴f(x)=sin(2x-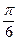 )+k+
)+k+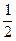
∵x∈
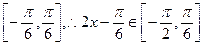 ………………8分
………………8分从而当2x-
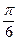 =
=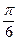 即x
即x =
=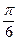 时fmax(x)=f(
时fmax(x)=f(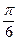 )=sin
)=sin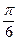 +k+
+k+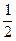 =k+1=
=k+1=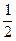
∴k=-
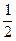 故f(x)=sin(2x-
故f(x)=sin(2x-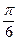 )…………………12分
)…………………12分
练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
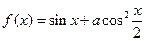 ,
, 为常数,
为常数,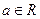 ,且
,且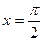 是方程
是方程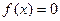 的解
的解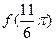 的值;
的值;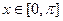 时,求函数
时,求函数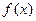 的值域.
的值域.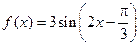 的图象为
的图象为 ,
,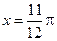 对称;②函数
对称;②函数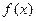 在区间
在区间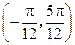 内是增函数;
内是增函数;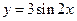 的图象向右平移
的图象向右平移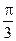 个单位长度可以得到图象
个单位长度可以得到图象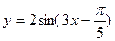 的图象,只需将函数
的图象,只需将函数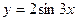 的图象( )
的图象( ) 个单位
个单位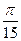 个单位
个单位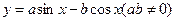 的一条对称轴的方程为
的一条对称轴的方程为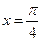 ,则以向量
,则以向量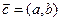 为方向向量的直线的倾斜角为 ( )
为方向向量的直线的倾斜角为 ( )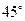 B
B .
.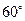 C.
C.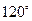 D.
D.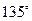
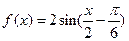 的最小正周期是
的最小正周期是 
 4
4
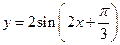
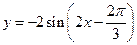
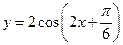
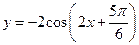
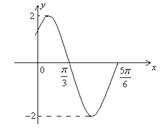
 的定义域是( ).
的定义域是( ).



 则函数
则函数 的最大值为_______
的最大值为_______