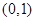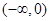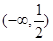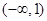题目内容
函数 在区间
在区间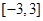 上的零点的个数为( )
上的零点的个数为( )
| A.3 | B.4 | C.5 | D.6 |
C.
解析试题分析:若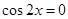 ,则由
,则由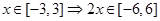 ,∴
,∴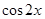 在
在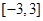 上有四个零点
上有四个零点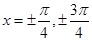 ,
,
又令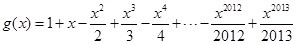 ,
,
∴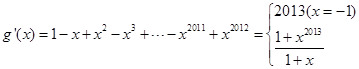 ,∴
,∴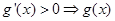 在
在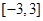 上单调递增,又∵
上单调递增,又∵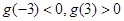 ,∴
,∴ 在
在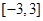 上有且只有一个零点,显然
上有且只有一个零点,显然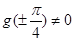 ,
,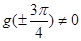 ,因此
,因此 的零点与前述
的零点与前述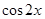 的四个零点不重合,∴
的四个零点不重合,∴ 共有
共有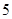 个零点.
个零点.
考点:1.数的运用;2.函数零点判断.

练习册系列答案
相关题目
设集合A={x|0≤x≤6},B={y|0≤y≤2},从A到B的对应法则f不是映射的是( ).
A. f:x→y=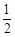 x x | B. f:x→y=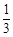 x x | C. f:x→y=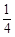 x x | D. f:x→y=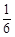 x x |
已知f(x)是定义在R上的奇函数,当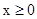 时,
时,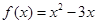 ,则函数
,则函数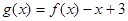 的零点的集合为
的零点的集合为
A.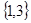 | B.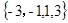 | C.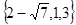 | D.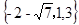 |
函数f(x)=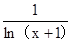 +
+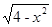 的定义域为( )
的定义域为( )
| A.[-2,0)∪(0,2] | B.(-1,0)∪(0,2] | C.[-2,2] | D.(-1,2] |
已知函数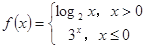 ,则
,则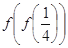 的值是( )
的值是( )
A. | B. | C.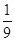 | D. |
函数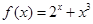 的零点所在区间为( )
的零点所在区间为( )
A.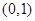 | B. | C.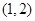 | D.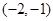 |
下列函数中,既是偶函数又在区间(0,+∞)上单调递减的是( )
A.y=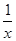 | B.y=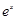 |
| C.y=-x2+2 | D.y=lg|x| |
下列函数中,定义域是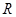 且为增函数的是( )
且为增函数的是( )
A.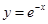 | B.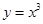 | C.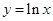 | D.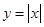 |
 是定义在R上的奇函数且单调递增,当
是定义在R上的奇函数且单调递增,当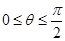 时,
时,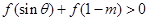 恒成立,则实数
恒成立,则实数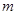 的取值范围是( )
的取值范围是( )