题目内容
函数 的单调减区间是 .
的单调减区间是 .
【答案】分析:先求出函数的定义域,再由复合函数判断单调性的同增异减性质判断即可
解答:解:∵x2+2x-3≥0∴原函数的定义域为:(-∞,-3]∪[1,+∞)
令z=x2+2x-3,原函数可表示为: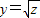 ,z=x2+2x-3
,z=x2+2x-3
∴单调减区间为:(-∞,-3]
故答案为:(-∞,-3].
点评:本题主要考查复合函数的单调性,注意同增异减的特性.
解答:解:∵x2+2x-3≥0∴原函数的定义域为:(-∞,-3]∪[1,+∞)
令z=x2+2x-3,原函数可表示为:
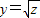 ,z=x2+2x-3
,z=x2+2x-3∴单调减区间为:(-∞,-3]
故答案为:(-∞,-3].
点评:本题主要考查复合函数的单调性,注意同增异减的特性.

练习册系列答案
相关题目
 的导数是
的导数是 ,则函数
,则函数 的单调减区间是 。
的单调减区间是 。 的导数是
的导数是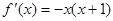 ,则函数
,则函数 的单调减区间是
的单调减区间是 B
B
 D
D 
 的单调减区间是
.
的单调减区间是
. 的单调减区间是( )
的单调减区间是( )  C.
C. D.
D.