题目内容
已知点A(0,6),圆C:x2+y2+10x+10y=0.
(1)求过点A且与圆C相切于原点O的圆C1的方程;
(2)求直线2x+3y+
-15=0被圆C1所截得的弦长.
(1)求过点A且与圆C相切于原点O的圆C1的方程;
(2)求直线2x+3y+
| 26 |
分析:(1)把圆的方程化为标准方程,找出圆心C的坐标,由所求圆与圆C相切与原点,得到两圆心与原点三点共线,由C和原点的坐标确定出三点共线的直线方程,得到所求圆的圆心在此直线上,由线段OA为所求圆中的弦,根据垂径定理得到圆心一定在弦AO的垂直平分线上,找出线段AO的垂直平分线,联立两直线方程得出方程组,求出方程组的解得到圆心的坐标,进而利用两点间的距离公式求出圆的半径,由圆心和半径写出圆的标准方程即可;
(2)由第一问求出的圆的方程得到圆心坐标和半径,利用点到直线的距离公式求出圆心到已知直线的距离即为弦心距,再由圆的半径,利用勾股定理求出弦长得一半,即可求出直线被圆所截得的弦长.
(2)由第一问求出的圆的方程得到圆心坐标和半径,利用点到直线的距离公式求出圆心到已知直线的距离即为弦心距,再由圆的半径,利用勾股定理求出弦长得一半,即可求出直线被圆所截得的弦长.
解答:( 本题满分(14分) )
解:(1)由x2+y2+10x+10y=0,得(x+5)2+(y+5)2=50,
所以圆C的圆心坐标(-5,-5),
而圆C1的圆心C1与圆心C、原点O共线,
故圆心C1在直线y=x上,又圆C1同时经过点O与点A(0,6),
所以圆心C1又在直线y=3上,则有:
,
解得:
,即圆心C1的坐标为(3,3),
又|OC1|=
=3
,即半径r=3
,
故所求圆C1的方程为(x-3)2+(y-3)2=18;
(2)∵圆心C1到直线2x+3y+
-15=0的距离d=
=
,
故所求的弦长为:2
=2
=8.
解:(1)由x2+y2+10x+10y=0,得(x+5)2+(y+5)2=50,
所以圆C的圆心坐标(-5,-5),
而圆C1的圆心C1与圆心C、原点O共线,
故圆心C1在直线y=x上,又圆C1同时经过点O与点A(0,6),
所以圆心C1又在直线y=3上,则有:
|
解得:
|
又|OC1|=
| 32+32 |
| 2 |
| 2 |
故所求圆C1的方程为(x-3)2+(y-3)2=18;
(2)∵圆心C1到直线2x+3y+
| 26 |
|6+9+
| ||
|
| 2 |
故所求的弦长为:2
| r2-d2 |
| 18-2 |
点评:此题考查了直线与圆相交的性质,涉及的知识有圆的标准方程,垂径定理,勾股定理,点到直线的距离公式,遇到直线与圆相交时,常常根据垂径定理作出所截得弦的弦心距,由弦长的一半,圆的半径及弦心距构造直角三角形,利用勾股定理来解决问题.

练习册系列答案
相关题目
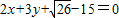 被圆C1所截得的弦长.
被圆C1所截得的弦长.