题目内容
(本题满分12分)解关于x的不等式ax2-2≥2x-ax(a∈R).
a=0时,x∈(-∞,-1); a>0时,x∈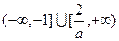 ;
;
-2<a<0时,x∈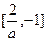 ; a<-2时,x∈
; a<-2时,x∈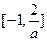 ;a=-2时,x∈{x|x=-1}.
;a=-2时,x∈{x|x=-1}.
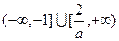 ;
;-2<a<0时,x∈
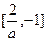 ; a<-2时,x∈
; a<-2时,x∈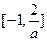 ;a=-2时,x∈{x|x=-1}.
;a=-2时,x∈{x|x=-1}.:原不等式可化为Ûax2+(a-2)x-2≥0,
(1)a=0时,x≤-1,即x∈(-∞,-1].
(2)a¹0时,不等式即为(ax-2)(x+1)≥0.
①a>0时,不等式化为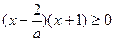 ,
,
当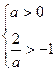 ,即a>0时,不等式解为
,即a>0时,不等式解为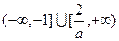 .
.
当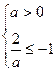 ,此时a不存在.
,此时a不存在.
②a<0时,不等式化为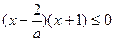 ,
,
当 ,即-2<a<0时,不等式解为
,即-2<a<0时,不等式解为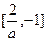
当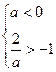 ,即a<-2时,不等式解为
,即a<-2时,不等式解为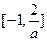 .
.
当 ,即a=-2时,不等式解为x=-1.
,即a=-2时,不等式解为x=-1.
综上: a=0时,x∈(-∞,-1); a>0时,x∈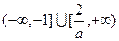 ;
;
-2<a<0时,x∈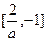 ; a<-2时,x∈
; a<-2时,x∈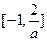 ;a=-2时,x∈{x|x=-1}.
;a=-2时,x∈{x|x=-1}.
(1)a=0时,x≤-1,即x∈(-∞,-1].
(2)a¹0时,不等式即为(ax-2)(x+1)≥0.
①a>0时,不等式化为
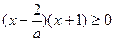 ,
,当
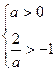 ,即a>0时,不等式解为
,即a>0时,不等式解为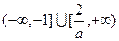 .
.当
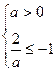 ,此时a不存在.
,此时a不存在.②a<0时,不等式化为
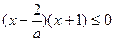 ,
,当
 ,即-2<a<0时,不等式解为
,即-2<a<0时,不等式解为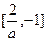
当
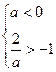 ,即a<-2时,不等式解为
,即a<-2时,不等式解为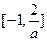 .
.当
 ,即a=-2时,不等式解为x=-1.
,即a=-2时,不等式解为x=-1.综上: a=0时,x∈(-∞,-1); a>0时,x∈
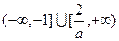 ;
;-2<a<0时,x∈
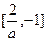 ; a<-2时,x∈
; a<-2时,x∈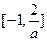 ;a=-2时,x∈{x|x=-1}.
;a=-2时,x∈{x|x=-1}.
练习册系列答案
相关题目
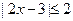 的解集与
的解集与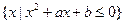 的解集相同,则( ).
的解集相同,则( ).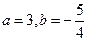
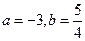
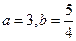
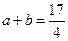
 ,求不等式
,求不等式 的解集.
的解集.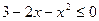 的解集是___________
的解集是___________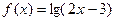 的定义域为集合M,函数
的定义域为集合M,函数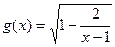 的定义域
的定义域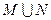 = .
= .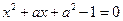 有一正根和一负根,则
有一正根和一负根,则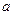 的取值范围为 .
的取值范围为 .
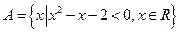 ,
, ,则
,则 =( )
=( )
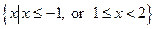


 ,
, ,则
,则 .
.