题目内容
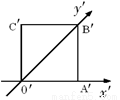
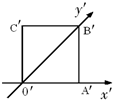 一水平放置的平面图形OABC,用斜二测画法画出它的直观图O′A′B′C′如图所示,此直观图恰好是一个边长为1的正方形,则原平面图形OABC的面积为
一水平放置的平面图形OABC,用斜二测画法画出它的直观图O′A′B′C′如图所示,此直观图恰好是一个边长为1的正方形,则原平面图形OABC的面积为分析:利用斜二测画法的过程把给出的直观图还原回原图形,即找到直观图中正方形的四个顶点在原图形中对应的点,用直线段连结后得到原四边形,然后直接利用平行四边形的面积公式求面积.
解答: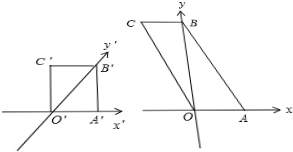 解:还原直观图为原图形如图,
解:还原直观图为原图形如图,
因为O′A′=1,所以O′B′=
,还原回原图形后,
OA=O′A′=1,OB=2O′B′=2
.
所以原图形的面积为1×2
=2
.
故答案为:2
.
 解:还原直观图为原图形如图,
解:还原直观图为原图形如图,因为O′A′=1,所以O′B′=
| 2 |
OA=O′A′=1,OB=2O′B′=2
| 2 |
所以原图形的面积为1×2
| 2 |
| 2 |
故答案为:2
| 2 |
点评:本题考查了平面图形直观图的画法,解答的关键是熟记斜二测画法的要点和步骤,从而还原得到原图形,求出面积,该类问题也可熟记一个二级结论,即
=2
.是基础题.
| S原 |
| S直 |
| 2 |

练习册系列答案
 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
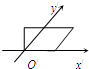 一水平放置的平面图形的直观图如图所示,则此平面图形的形状是( )
一水平放置的平面图形的直观图如图所示,则此平面图形的形状是( )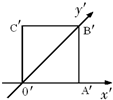 (2013•泉州模拟)一水平放置的平面图形OABC,用斜二测画法画出它的直观图O'A'B'C'如图所示,此直观图恰好是一个边长为2的正方形,则原平面图形OABC的面积为
(2013•泉州模拟)一水平放置的平面图形OABC,用斜二测画法画出它的直观图O'A'B'C'如图所示,此直观图恰好是一个边长为2的正方形,则原平面图形OABC的面积为 ,用斜二测画法画出它的直观图
,用斜二测画法画出它的直观图 如图所示,此直观图恰好是一个边长为
如图所示,此直观图恰好是一个边长为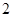 的正方形,则原平面图形
的正方形,则原平面图形