题目内容
已知非零向量e1,e2,a,b满足a=2e1-e2,b=ke1+e2.
(1)若e1与e2不共线,a与b是共线,求实数k的值;
(2)是否存在实数k,使得a与b不共线,e1与e2是共线?若存在,求出k的值,否则说明理由.
解:(1)由 =λ
=λ ,得2
,得2 =λk
=λk +λ
+λ ,而
,而 与
与 不共线,
不共线,
∴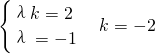 ;
;
(2)若 与
与 是共线,则
是共线,则 =λ
=λ ,有
,有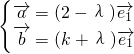
∵ ,
, ,
, 为非零向量,∴λ≠2且λ≠-k,
为非零向量,∴λ≠2且λ≠-k,
∴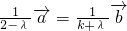 ,即
,即 ,这时a与b共线,
,这时a与b共线,
∴不存在实数k满足题意.
分析:(1)利用向量共线的充要条件列出方程据平面向量的基本定理求出k.
(2)利用向量共线设出等式,将 ,
, 用不共线的基底
用不共线的基底 表示,得到矛盾.
表示,得到矛盾.
点评:本题考查向量共线的充要条件、平面向量的基本定理.
 =λ
=λ ,得2
,得2 =λk
=λk +λ
+λ ,而
,而 与
与 不共线,
不共线,∴
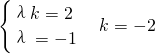 ;
;(2)若
 与
与 是共线,则
是共线,则 =λ
=λ ,有
,有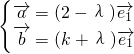
∵
 ,
, ,
, 为非零向量,∴λ≠2且λ≠-k,
为非零向量,∴λ≠2且λ≠-k,∴
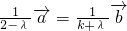 ,即
,即 ,这时a与b共线,
,这时a与b共线,∴不存在实数k满足题意.
分析:(1)利用向量共线的充要条件列出方程据平面向量的基本定理求出k.
(2)利用向量共线设出等式,将
 ,
, 用不共线的基底
用不共线的基底 表示,得到矛盾.
表示,得到矛盾.点评:本题考查向量共线的充要条件、平面向量的基本定理.

练习册系列答案
相关题目