题目内容
 在正方形内有一扇形(见阴影部分),点P随意等可能落在正方形内,则这点落在扇形外且在正方形内的概率为
在正方形内有一扇形(见阴影部分),点P随意等可能落在正方形内,则这点落在扇形外且在正方形内的概率为1-
| π |
| 4 |
1-
.| π |
| 4 |
分析:确定正方形、扇形的面积,结合几何概型的计算公式即可求得点落在扇形外且在正方形内的概率.
解答:解:令正方形的边长为a,则S正方形=a2,
则扇形所在圆的半径也为a,则S扇形=
πa2
则黄豆落在阴影区域内的概率P=1-
=1-
.
故答案为:1-
.
则扇形所在圆的半径也为a,则S扇形=
| 1 |
| 4 |
则黄豆落在阴影区域内的概率P=1-
| S扇形 |
| S正方形 |
| π |
| 4 |
故答案为:1-
| π |
| 4 |
点评:本题主要考查扇形面积公式、几何概型等基础知识,考查运算求解能力,考查数形结合思想.解题的关键是要求出阴影部分的面积及正方形的面积,属于基础题.

练习册系列答案
相关题目
 如图,在正方形内有一扇形(见阴影部分),扇形对应的圆心是正方形的一顶点,半径为正方形的边长.在这个图形上随机撒一粒黄豆,它落在扇形外正方形内的概率为( )(用分数表示)
如图,在正方形内有一扇形(见阴影部分),扇形对应的圆心是正方形的一顶点,半径为正方形的边长.在这个图形上随机撒一粒黄豆,它落在扇形外正方形内的概率为( )(用分数表示)A、
| ||
B、
| ||
C、1-
| ||
D、
|
 如图,在正方形内有一扇形(见阴影部分),扇形对应的圆心是正方形的一顶点,半径为正方形的边长.在这个图形上随机撒一粒黄豆,它落在扇形外正方形内的概率为
如图,在正方形内有一扇形(见阴影部分),扇形对应的圆心是正方形的一顶点,半径为正方形的边长.在这个图形上随机撒一粒黄豆,它落在扇形外正方形内的概率为
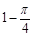 B.
B. C.
C. D.
D.
